Shuffled total least squares

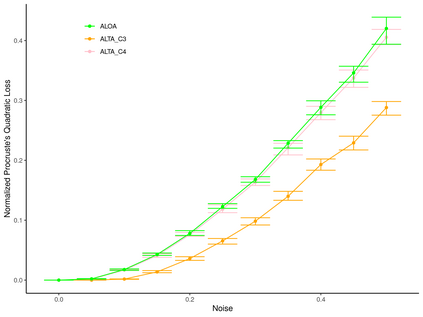
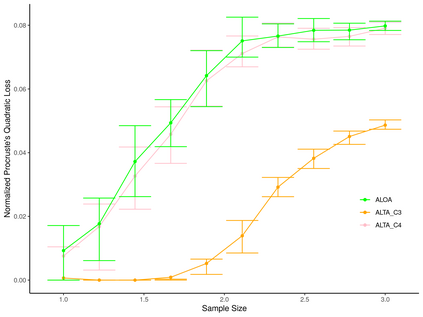
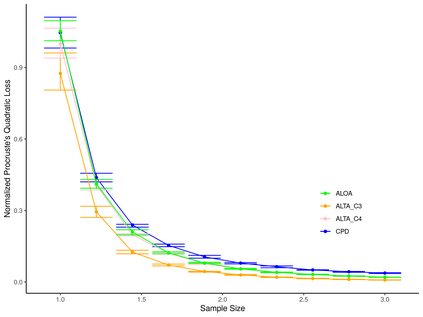
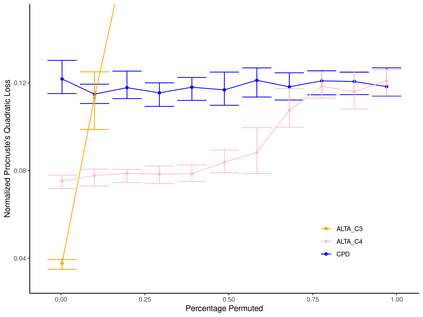
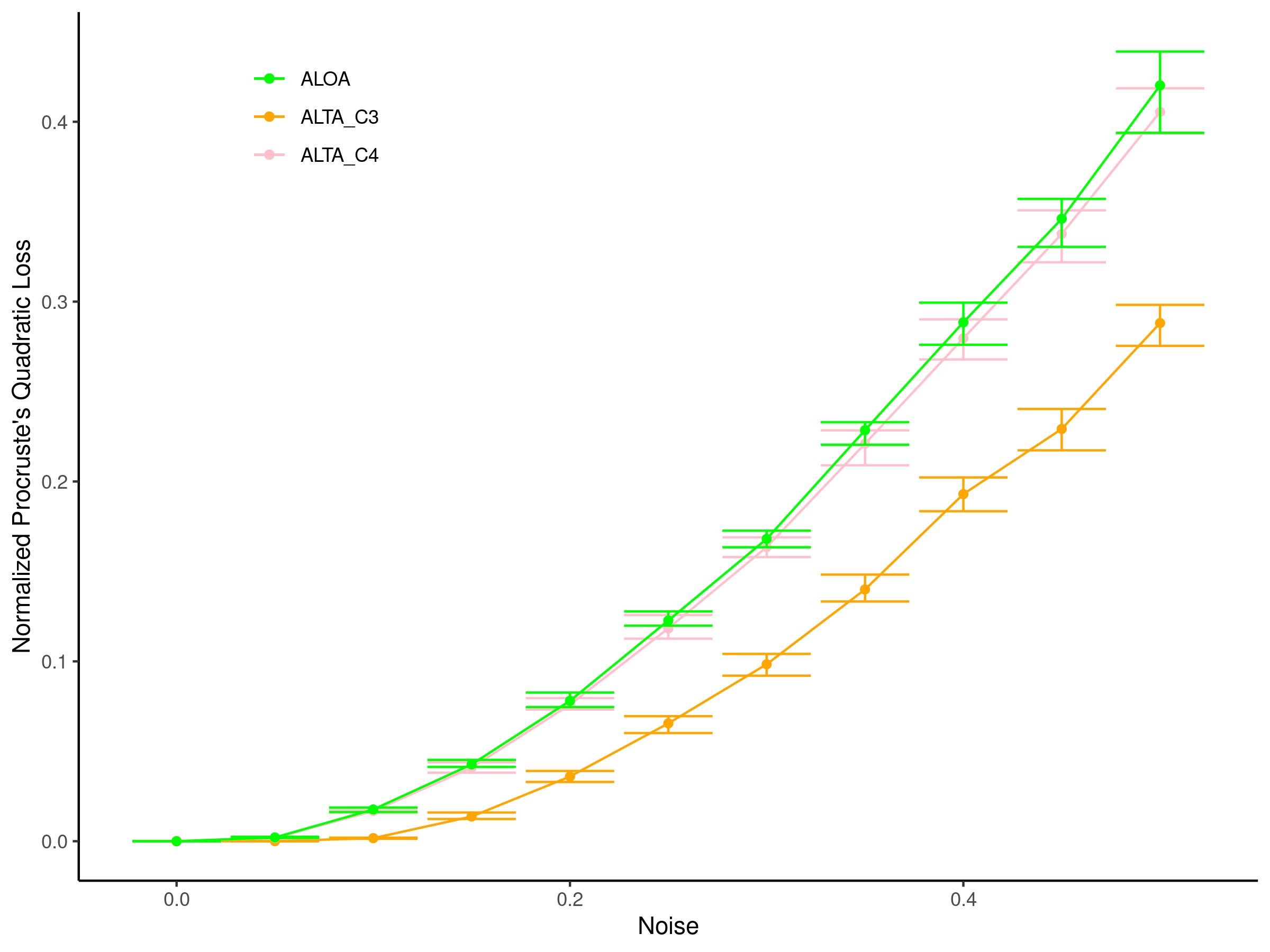
Linear regression with shuffled labels and with a noisy latent design matrix arises in many correspondence recovery problems. We propose a total least-squares approach to the problem of estimating the underlying true permutation and provide an upper bound to the normalized Procrustes quadratic loss of the estimator. We also provide an iterative algorithm to approximate the estimator and demonstrate its performance on simulated data.