Hamiltonian Dynamics of Bayesian Inference Formalised by Arc Hamiltonian Systems

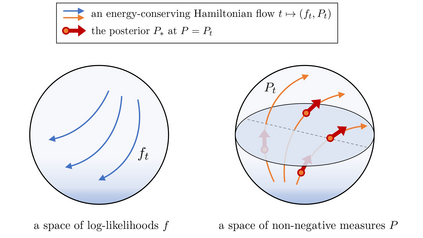
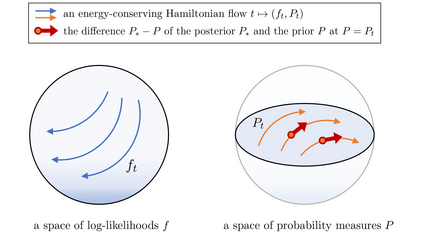
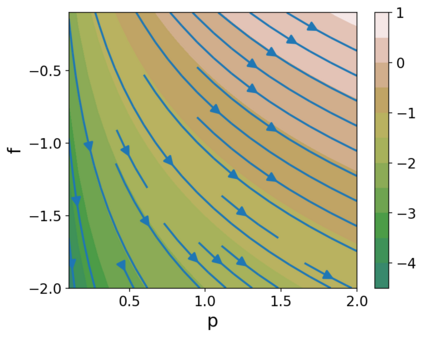
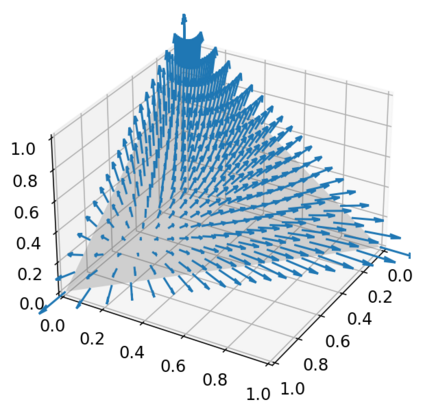
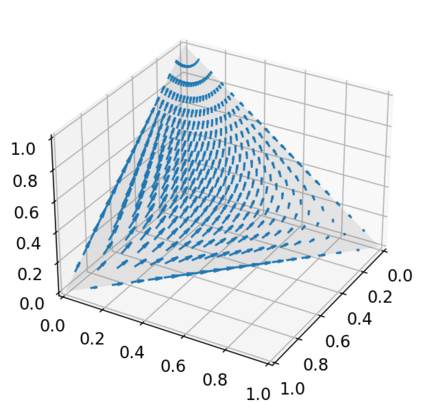
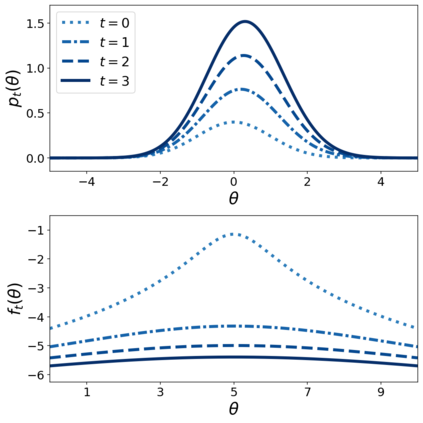
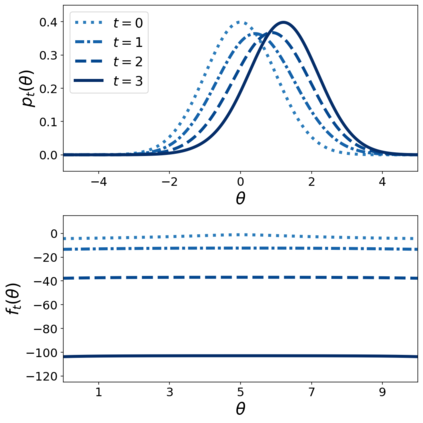
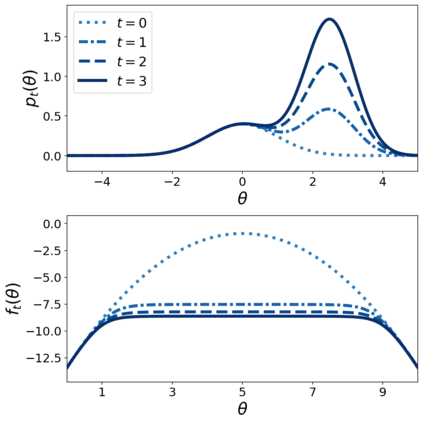
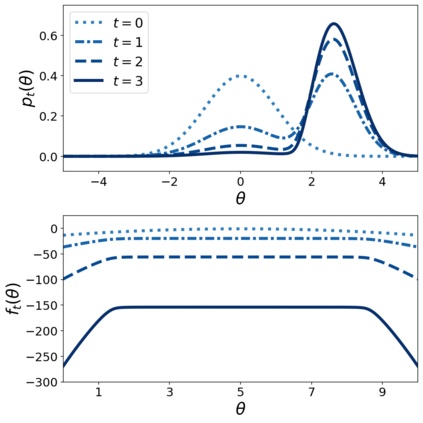
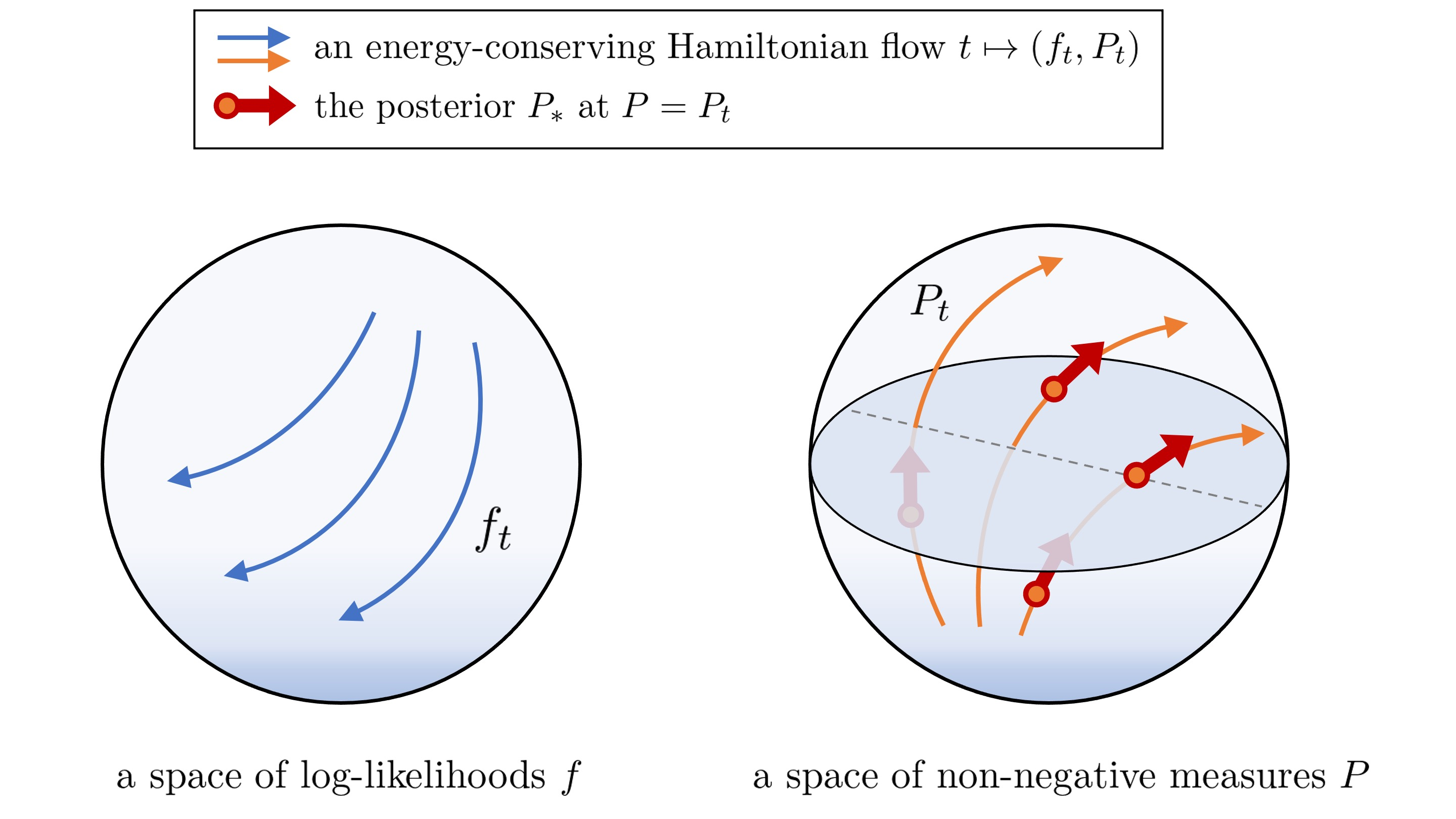
This paper makes two theoretical contributions. First, we establish a novel class of Hamiltonian systems, called arc Hamiltonian systems, for saddle Hamiltonian functions over infinite-dimensional metric spaces. Arc Hamiltonian systems generate a flow that satisfies the law of conservation of energy everywhere in a metric space. They are governed by an extension of Hamilton's equation formulated based on (i) the framework of arc fields and (ii) an infinite-dimensional gradient, termed the arc gradient, of a Hamiltonian function. We derive conditions for the existence of a flow generated by an arc Hamiltonian system, showing that they reduce to local Lipschitz continuity of the arc gradient under sufficient regularity. Second, we present two Hamiltonian functions, called the cumulant generating functional and the centred cumulant generating functional, over a metric space of log-likelihoods and measures. The former characterises the posterior of Bayesian inference as a part of the arc gradient that induces a flow of log-likelihoods and non-negative measures. The latter characterises the difference of the posterior and the prior as a part of the arc gradient that induces a flow of log-likelihoods and probability measures. Our results reveal an implication of the belief updating mechanism from the prior to the posterior as an infinitesimal change of a measure in the infinite-dimensional Hamiltonian flows.