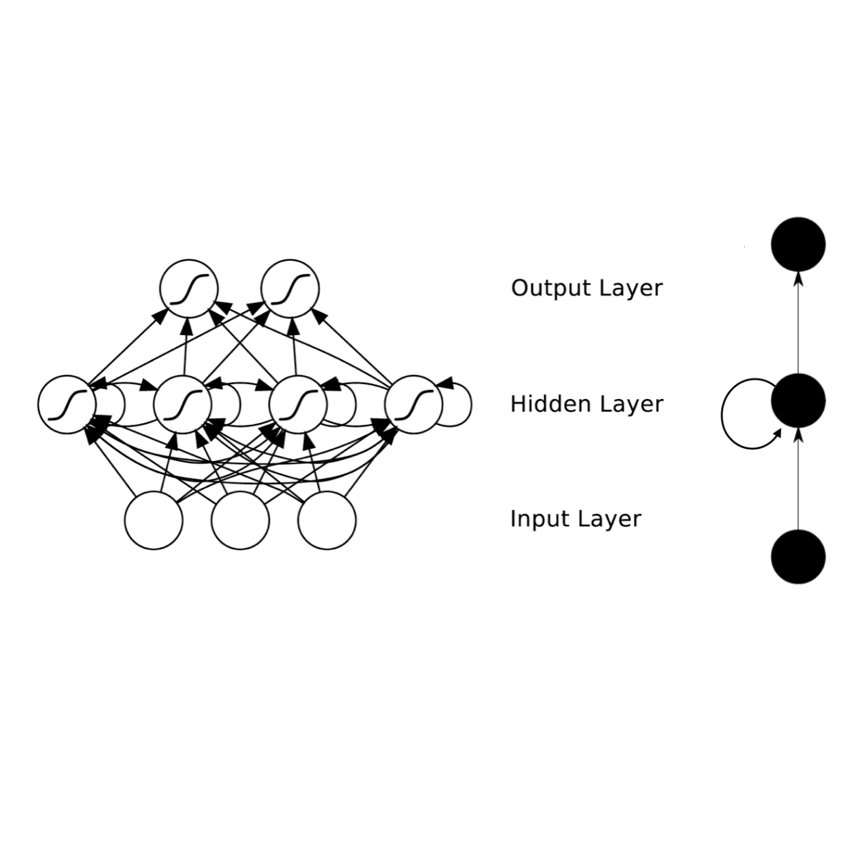
Micro-segmentation of customers in the finance sector is a non-trivial task and has been an atypical omission from recent scientific literature. Where traditional segmentation classifies customers based on coarse features such as demographics, micro-segmentation depicts more nuanced differences between individuals, bringing forth several advantages including the potential for improved personalization in financial services. AI and representation learning offer a unique opportunity to solve the problem of micro-segmentation. Although ubiquitous in many industries, the proliferation of AI in sensitive industries such as finance has become contingent on the explainability of deep models. We had previously solved the micro-segmentation problem by extracting temporal features from the state space of a recurrent neural network (RNN). However, due to the inherent opacity of RNNs our solution lacked an explanation. In this study, we address this issue by extracting a symbolic explanation for our model and providing an interpretation of our temporal features. For the explanation, we use a linear regression model to reconstruct the features in the state space with high fidelity. We show that our linear regression coefficients have not only learned the rules used to recreate the features, but have also learned the relationships that were not directly evident in the raw data. Finally, we propose a novel method to interpret the dynamics of the state space by using the principles of inverse regression and dynamical systems to locate and label a set of attractors.
翻译:金融部门客户的微分化是一个非边际任务,是最近科学文献中一个典型的遗漏。传统分化根据人口学等粗化特征对客户进行分类,而微分分化则显示个人之间的差别更加细化,从而带来若干好处,包括改善金融服务个人化的潜力。AI和代表学习为解决微观分化问题提供了一个独特的机会。虽然在许多行业中,AI在金融等敏感行业中普遍存在,但这种扩散取决于深层模型的可解释性。我们以前曾通过从经常神经网络(NNNN)的状态中提取时间特征来解决微分化问题。然而,由于个人之间固有的不透明性,我们的解决办法缺乏解释。在本研究中,我们通过对模型作出象征性的解释和对时间特征的解释来解决这一问题。对于解释,我们使用线性回归模型来重建国家空间的特征,高度忠诚。我们以前通过从经常的神经网络(RNNN)的状态空间空间中提取时间特征来解决微观分层的分层分层分层分层分层分层分层分层分层分层问题。我们不仅通过直线性回归系数,而且从原始的轨法中学习了一种分界法,最后还利用了一种分层法来重新解释。我们所学到一种分层的分层的分层结构的分层的分层的分层的分层法系,我们所学到一种分层的分层的分层的分层的分层的分层的分层的分层的分层的分层的分层的分层的分层的分层的分层的分层的分层法。