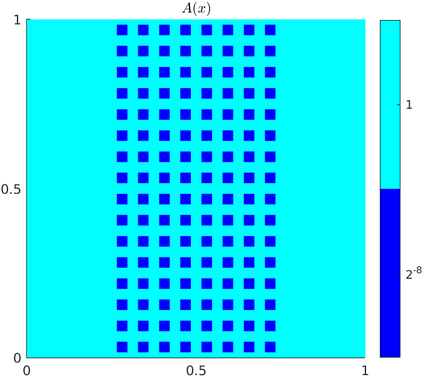
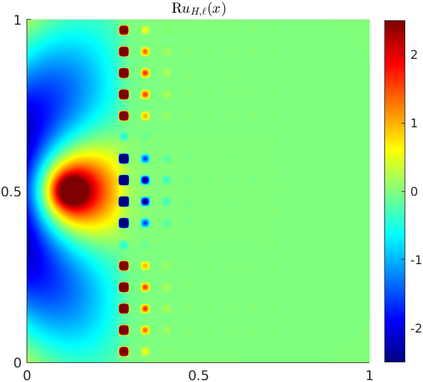
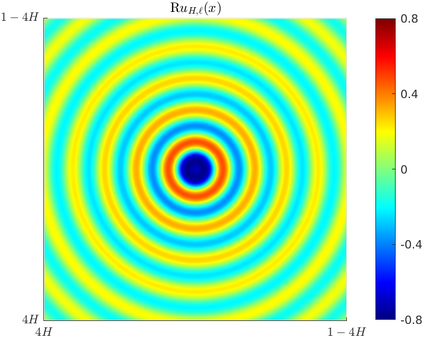
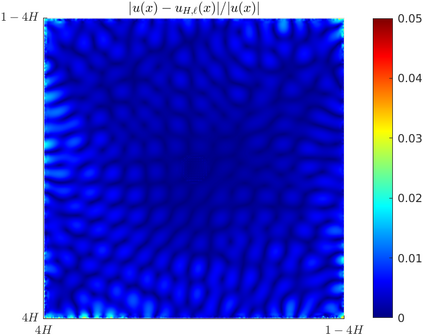
We propose a novel variant of the Localized Orthogonal Decomposition (LOD) method for time-harmonic scattering problems of Helmholtz type with high wavenumber $\kappa$. On a coarse mesh of width $H$, the proposed method identifies local finite element source terms that yield rapidly decaying responses under the solution operator. They can be constructed to high accuracy from independent local snapshot solutions on patches of width $\ell H$ and are used as problem-adapted basis functions in the method. In contrast to the classical LOD and other state-of-the-art multi-scale methods, the localization error decays super-exponentially as the oversampling parameter $\ell$ is increased. This implies that optimal convergence is observed under the substantially relaxed oversampling condition $\ell \gtrsim (\log \tfrac{\kappa}{H})^{(d-1)/d}$ with $d$ denoting the spatial dimension. Numerical experiments demonstrate the significantly improved offline and online performance of the method also in the case of heterogeneous media and perfectly matched layers.
翻译:我们建议了一种新颖的可变方程式,用于使用高波数的赫尔莫霍茨型的局部矫形分解(LOD)方法,用于处理高波数的时-调散问题。在宽度为$H的粗略网块上,拟议方法确定了在溶解操作器下产生快速衰减反应的局部有限元素源术语。这些术语可以从宽度为$@ellH$的独立本地快照解决方案中以高精度构建,并用作该方法中的问题调适基函数。与古典LOD和其他最先进的多尺度方法相比,本地化错误会随着过度采样参数$\ell美元的增加而发生超爆炸性衰减。这意味着在大幅放松的超标条件$\ell\gtrsim (\log\ tfrac kppa ⁇ H}\(d-1)/d}中观察到最佳趋同度的趋同度,在混合媒体和完美层中,该方法的离线和在线性性表现也显著改善。