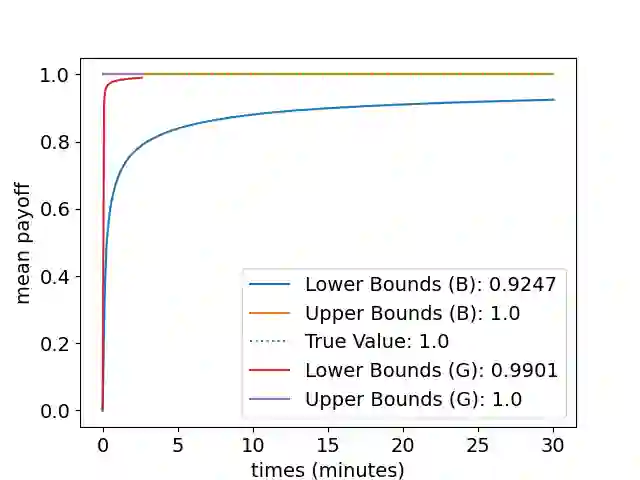
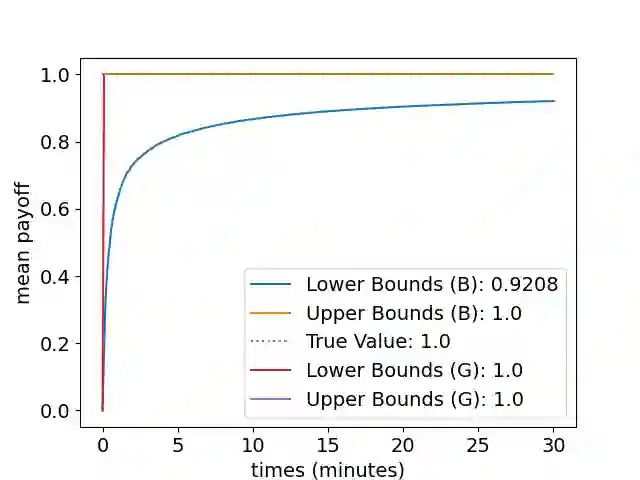
Markov decision processes (MDP) and continuous-time MDP (CTMDP) are the fundamental models for non-deterministic systems with probabilistic uncertainty. Mean payoff (a.k.a. long-run average reward) is one of the most classic objectives considered in their context. We provide the first algorithm to compute mean payoff probably approximately correctly in unknown MDP; further, we extend it to unknown CTMDP. We do not require any knowledge of the state space, only a lower bound on the minimum transition probability, which has been advocated in literature. In addition to providing probably approximately correct (PAC) bounds for our algorithm, we also demonstrate its practical nature by running experiments on standard benchmarks.
翻译:Markov决策程序和连续时间MDP(CTMDP)是具有概率不确定性的非决定性系统的基本模式。平均报酬(a.k.a.长期平均奖励)是其背景中考虑的最经典目标之一。我们提供了第一个算法,在未知的MDP中计算平均报酬可能大致正确;此外,我们将其扩大到未知的CTMDP。我们不需要任何关于国家空间的知识,而只需要文献中提倡的关于最低过渡概率的较低约束。除了为我们的算法提供可能大致正确的(PAC)界限外,我们还通过在标准基准上进行实验来证明其实用性。