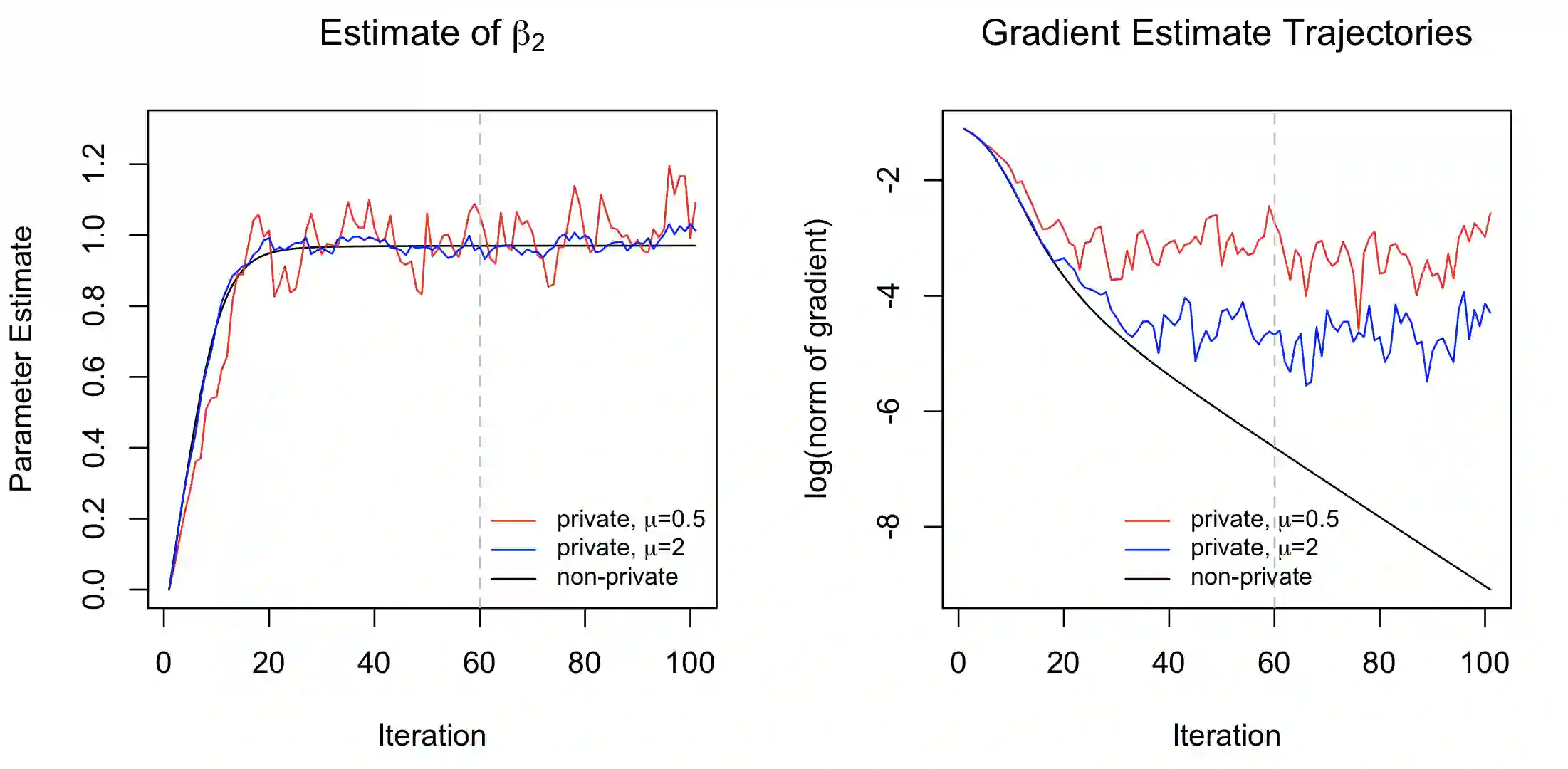
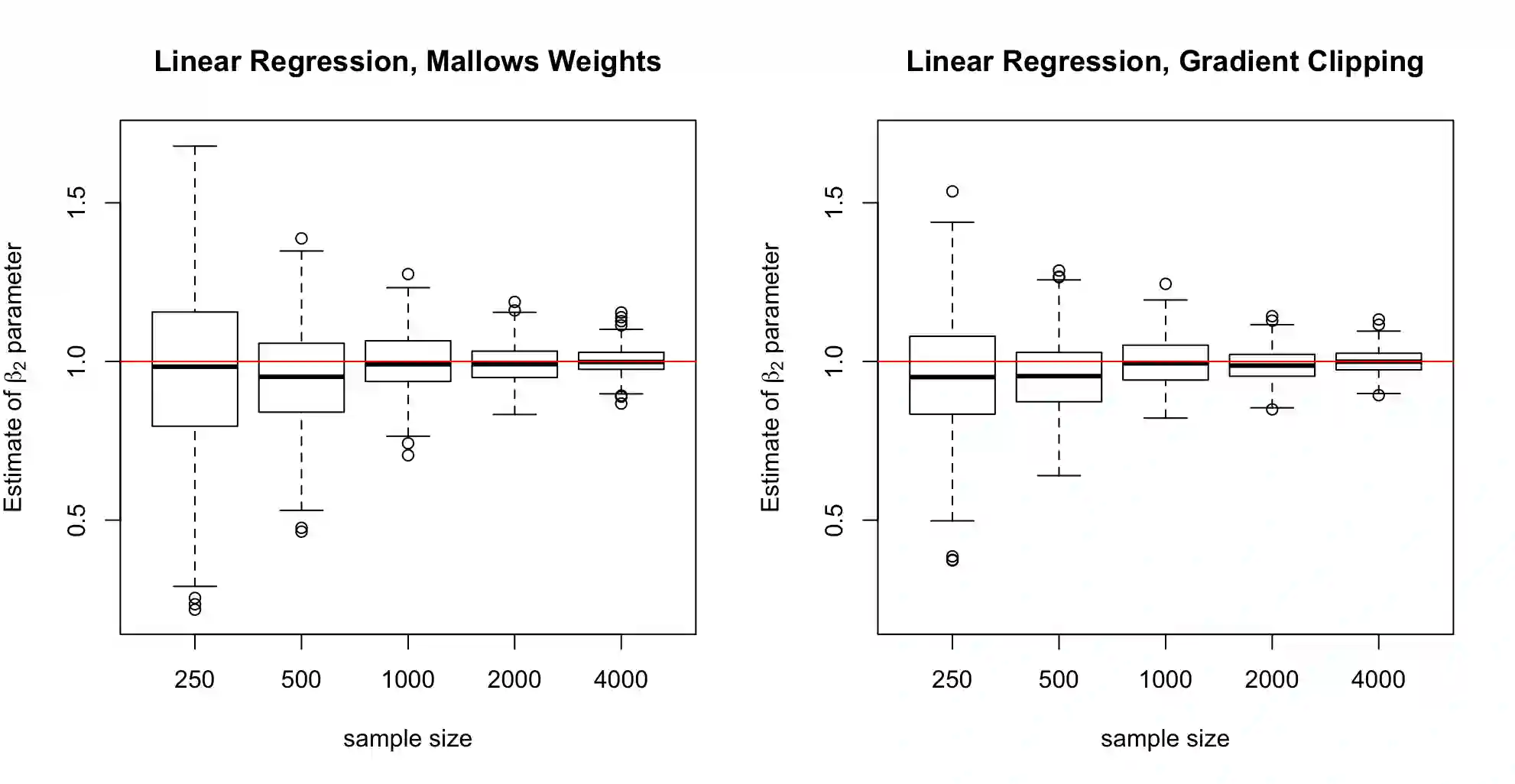
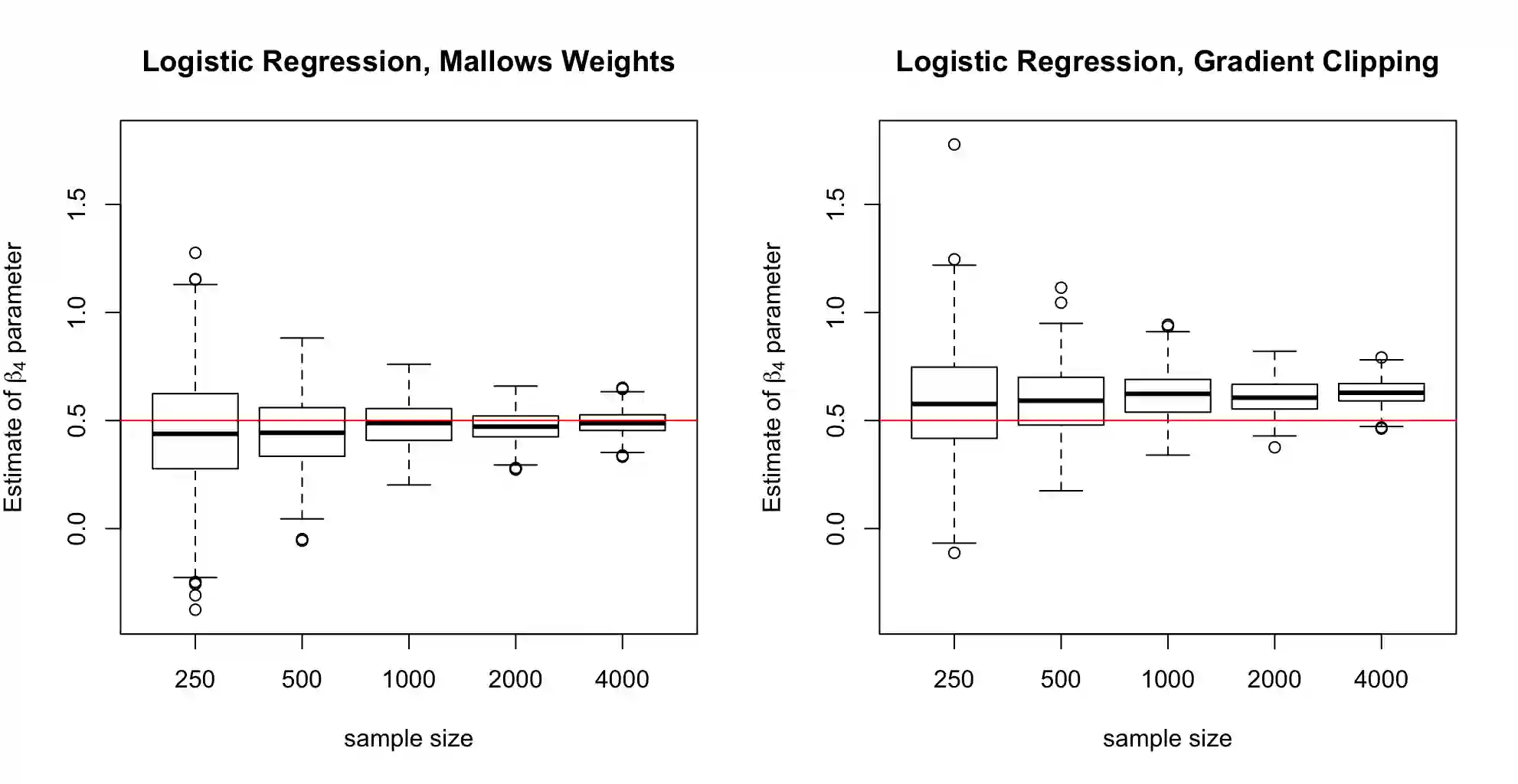
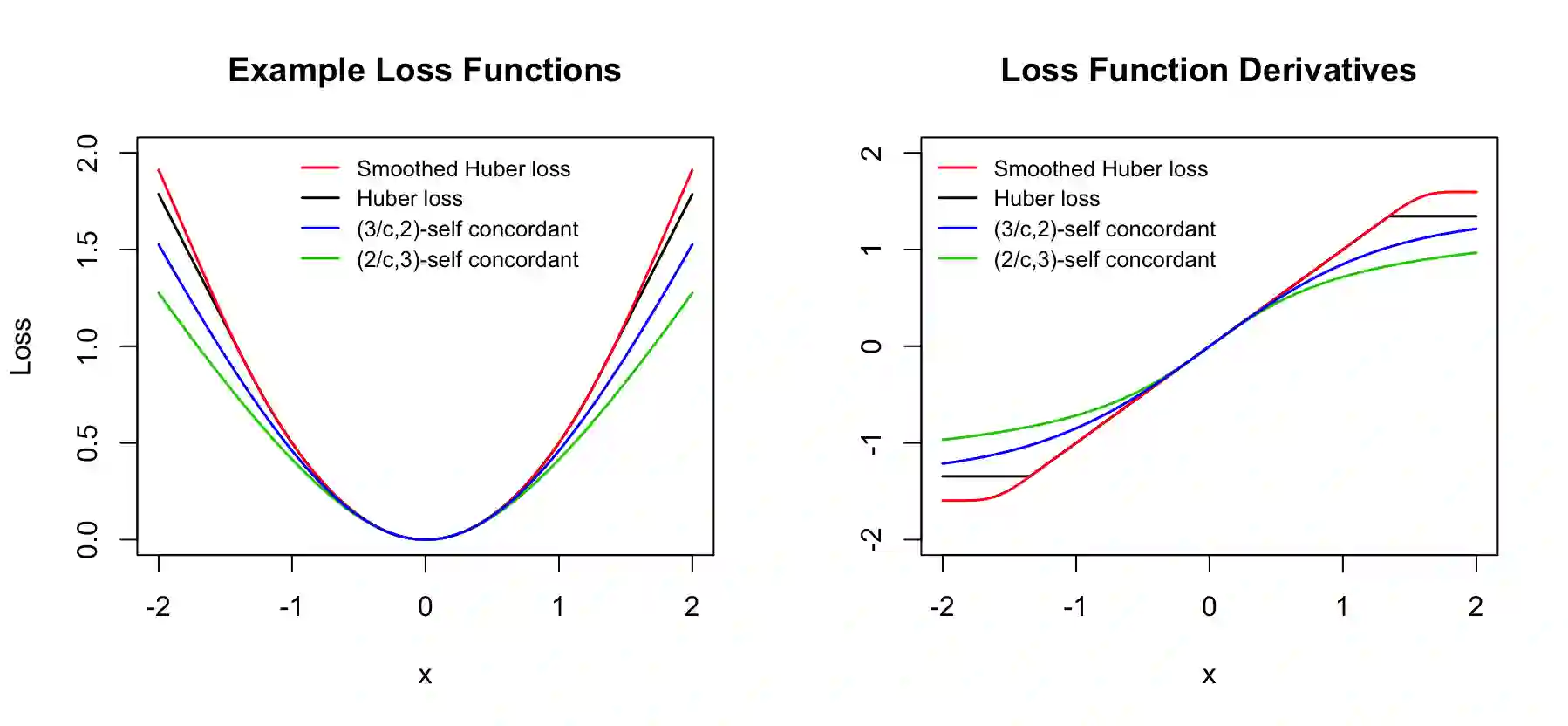
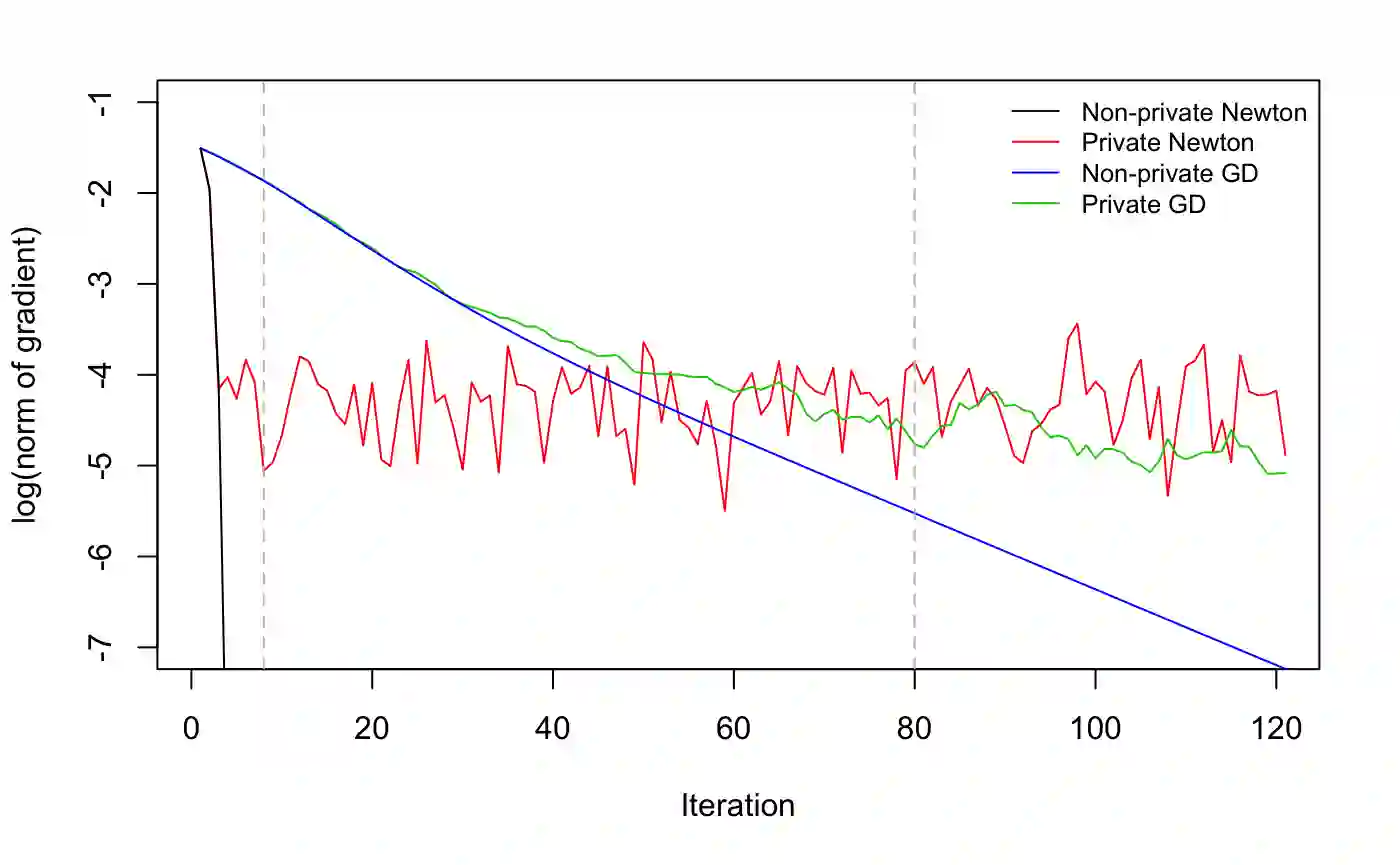
We propose a general optimization-based framework for computing differentially private M-estimators and a new method for constructing differentially private confidence regions. Firstly, we show that robust statistics can be used in conjunction with noisy gradient descent or noisy Newton methods in order to obtain optimal private estimators with global linear or quadratic convergence, respectively. We establish local and global convergence guarantees, under both local strong convexity and self-concordance, showing that our private estimators converge with high probability to a nearly optimal neighborhood of the non-private M-estimators. Secondly, we tackle the problem of parametric inference by constructing differentially private estimators of the asymptotic variance of our private M-estimators. This naturally leads to approximate pivotal statistics for constructing confidence regions and conducting hypothesis testing. We demonstrate the effectiveness of a bias correction that leads to enhanced small-sample empirical performance in simulations. We illustrate the benefits of our methods in several numerical examples.
翻译:我们提议了一个基于优化的总体框架,用于计算差别化的私人M估计数字,并采用新的方法构建差别化的私人信任区域。首先,我们表明,可以结合噪音的梯度下降或噪音的牛顿方法使用稳健的统计数据,以便分别获得具有全球线性或二次趋同的最佳私人估计数字。我们在地方强力凝聚和自我协调下建立了地方和全球的趋同保证,表明我们的私人估计数字极有可能与非私人M估计数字的近乎最佳的邻区汇合在一起。第二,我们通过建立差别化的私人估计数字模型来应对参数的误差问题。这自然导致建立信任区域和进行假设测试的关键统计数字的近似值。我们通过几个数字例子来展示出我们方法的效益。我们通过几个数字例子来说明我们方法的效益。