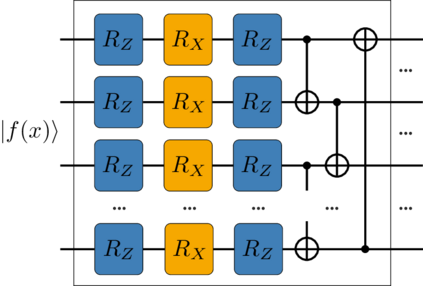
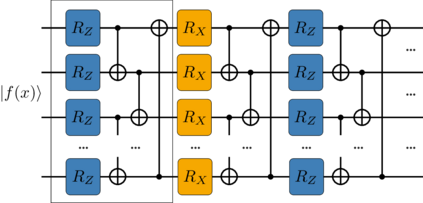
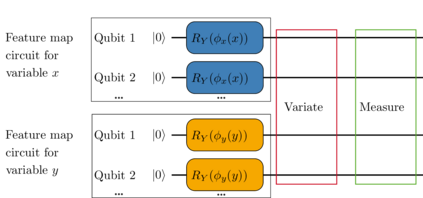
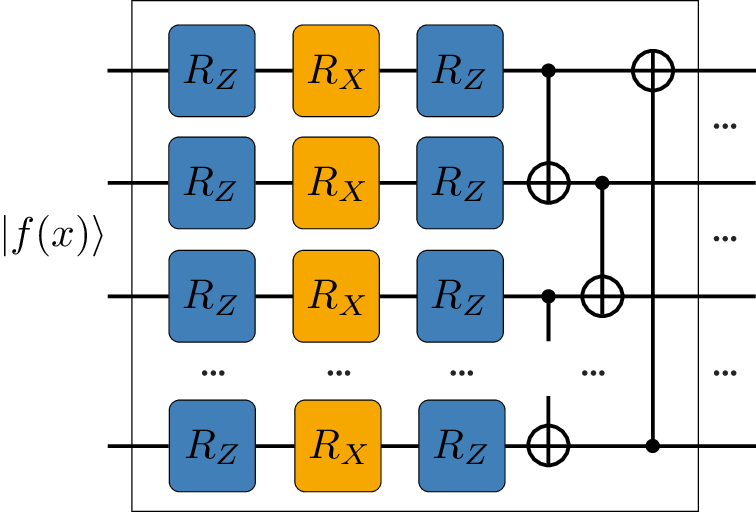
In this work, we solve differential equations using quantum Chebyshev feature maps. We propose a tensor product over a summation of Pauli-Z operators as a change in the measurement observables resulting in improved accuracy and reduced computation time for initial value problems processed by floating boundary handling. This idea has been tested on solving the complex dynamics of a Riccati equation as well as on a system of differential equations. Furthermore, a second-order differential equation is investigated in which we propose adding entangling layers to improve accuracy without increasing the variational parameters. Additionally, a modified self-adaptivity approach of physics-informed neural networks is incorporated to balance the multi-objective loss function. Finally, a new quantum circuit structure is proposed to approximate multivariable functions, tested on solving a 2D Poisson's equation.
翻译:暂无翻译