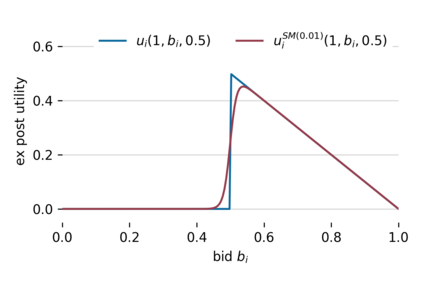
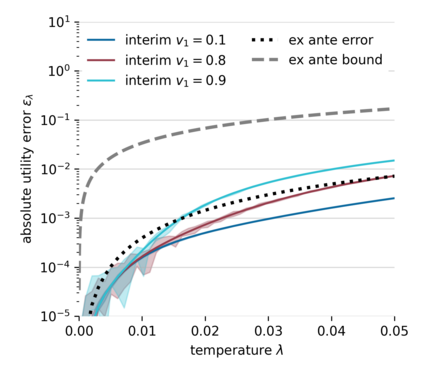
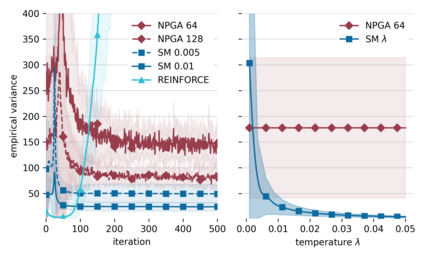
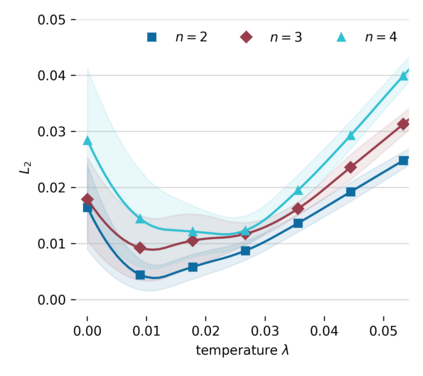
Understanding and analyzing markets is crucial, yet analytical equilibrium solutions remain largely infeasible. Recent breakthroughs in equilibrium computation rely on zeroth-order policy gradient estimation. These approaches commonly suffer from high variance and are computationally expensive. The use of fully differentiable simulators would enable more efficient gradient estimation. However, the discrete allocation of goods in economic simulations is a non-differentiable operation. This renders the first-order Monte Carlo gradient estimator inapplicable and the learning feedback systematically misleading. We propose a novel smoothing technique that creates a surrogate market game, in which first-order methods can be applied. We provide theoretical bounds on the resulting bias which justifies solving the smoothed game instead. These bounds also allow choosing the smoothing strength a priori such that the resulting estimate has low variance. Furthermore, we validate our approach via numerous empirical experiments. Our method theoretically and empirically outperforms zeroth-order methods in approximation quality and computational efficiency.
翻译:理解和分析市场至关重要,但是分析均衡解决方案仍然很难。最近对均衡计算的突破依赖于零阶策略梯度估计。这些方法通常存在高方差并且计算代价高。完全可微分的模拟器的使用将实现更高效的梯度估计。但是,经济模拟中物品的离散分配是一种不可微分的操作。这使得一阶蒙特卡洛梯度估计器不适用于该问题,而学习反馈系统性地误导人们。我们提出了一种新颖的平滑技术,创造了一个代理市场游戏,可以应用一阶方法。我们提供了关于结果偏差的理论界限,其中平滑后的游戏可以被解决。这些界限还允许在先选择平滑强度,使得估计结果方差低。此外,我们通过多个实证实验验证了我们的方法。我们的方法在逼近质量和计算效率方面理论和实证上优于零阶方法。