Gating creates slow modes and controls phase-space complexity in GRUs and LSTMs

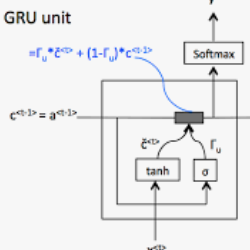
Recurrent neural networks (RNNs) are powerful dynamical models for data with complex temporal structure. However, training RNNs has traditionally proved challenging due to exploding or vanishing of gradients. RNN models such as LSTMs and GRUs (and their variants) significantly mitigate the issues associated with training RNNs by introducing various types of {\it gating} units into the architecture. While these gates empirically improve performance, how the addition of gates influences the dynamics and trainability of GRUs and LSTMs is not well understood. Here, we take the perspective of studying randomly-initialized LSTMs and GRUs as dynamical systems, and ask how the salient dynamical properties are shaped by the gates. We leverage tools from random matrix theory and mean-field theory to study the state-to-state Jacobians of GRUs and LSTMs. We show that the update gate in the GRU and the forget gate in the LSTM can lead to an accumulation of slow modes in the dynamics. Moreover, the GRU update gate can poise the system at a marginally stable point. The reset gate in the GRU and the output and input gates in the LSTM control the spectral radius of the Jacobian, and the GRU reset gate also modulates the complexity of the landscape of fixed-points. Furthermore, for the GRU we obtain a phase diagram describing the statistical properties of fixed-points. Finally, we provide some preliminary comparison of training performance to the various dynamical regimes, which will be investigated elsewhere. The techniques introduced here can be generalized to other RNN architectures to elucidate how various architectural choices influence the dynamics and potentially discover novel architectures.