Sparsistent Model Discovery

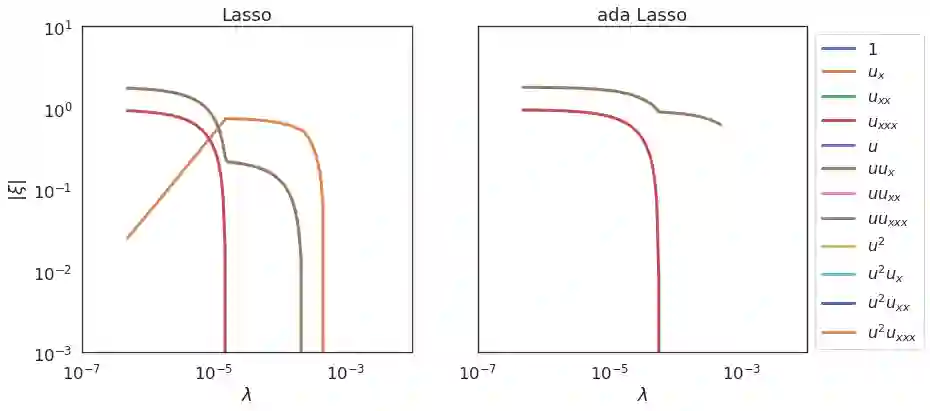
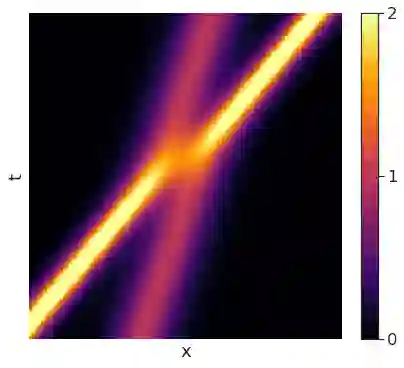
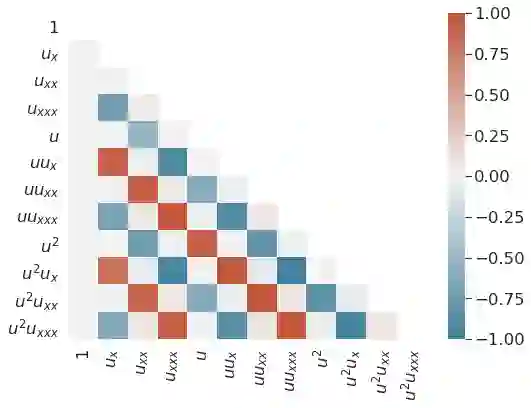
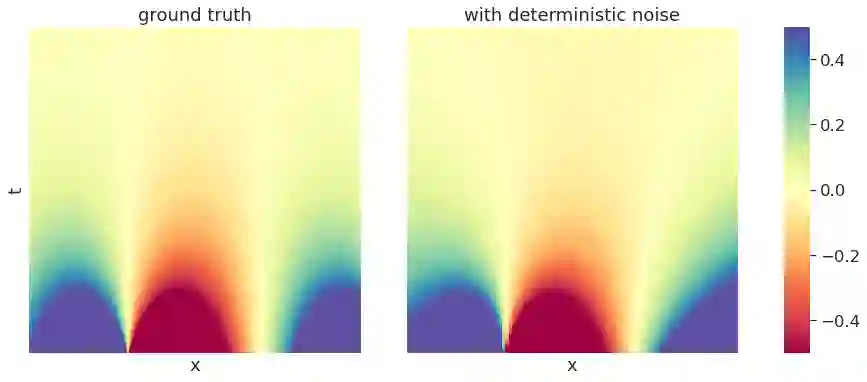
Discovering the partial differential equations underlying a spatio-temporal datasets from very limited observations is of paramount interest in many scientific fields. However, it remains an open question to know when model discovery algorithms based on sparse regression can actually recover the underlying physical processes. We trace back the poor of performance of Lasso based model discovery algorithms to its potential variable selection inconsistency: meaning that even if the true model is present in the library, it might not be selected. By first revisiting the irrepresentability condition (IRC) of the Lasso, we gain some insights of when this might occur. We then show that the adaptive Lasso will have more chances of verifying the IRC than the Lasso and propose to integrate it within a deep learning model discovery framework with stability selection and error control. Experimental results show we can recover several nonlinear and chaotic canonical PDEs with a single set of hyperparameters from a very limited number of samples at high noise levels.