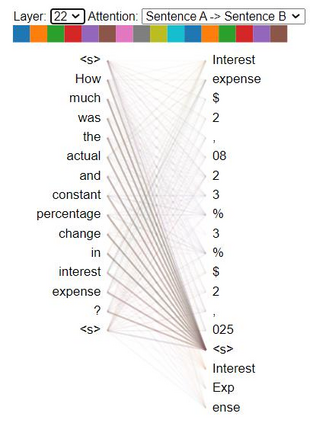
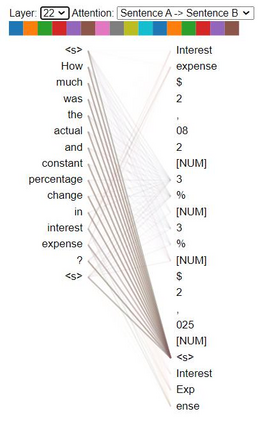
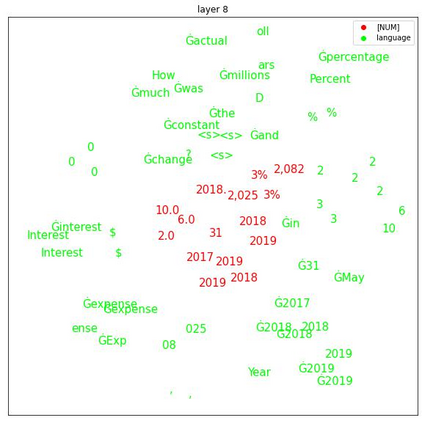
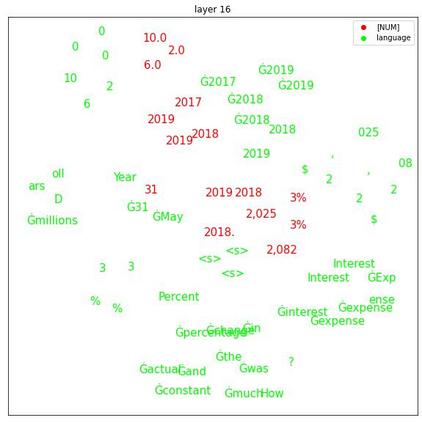
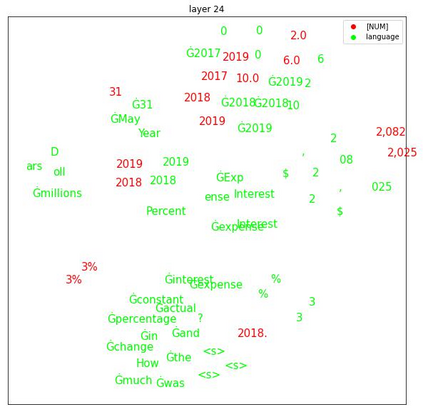
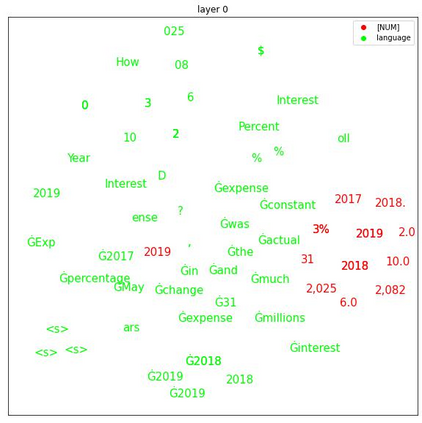
Transformers are widely used in NLP tasks. However, current approaches to leveraging transformers to understand language expose one weak spot: Number understanding. In some scenarios, numbers frequently occur, especially in semi-structured data like tables. But current approaches to rich-number tasks with transformer-based language models abandon or lose some of the numeracy information - e.g., breaking numbers into sub-word tokens - which leads to many number-related errors. In this paper, we propose the LUNA framework which improves the numerical reasoning and calculation capabilities of transformer-based language models. With the number plugin of NumTok and NumBed, LUNA represents each number as a whole to model input. With number pre-training, including regression loss and model distillation, LUNA bridges the gap between number and vocabulary embeddings. To the best of our knowledge, this is the first work that explicitly injects numeracy capability into language models using Number Plugins. Besides evaluating toy models on toy tasks, we evaluate LUNA on three large-scale transformer models (RoBERTa, BERT, TabBERT) over three different downstream tasks (TATQA, TabFact, CrediTrans), and observe the performances of language models are constantly improved by LUNA. The augmented models also improve the official baseline of TAT-QA (EM: 50.15 -> 59.58) and achieve SOTA performance on CrediTrans (F1 = 86.17).
翻译:在NLP任务中广泛使用变压器。然而,目前利用变压器来理解语言的方法暴露了一个薄弱点:数字理解。在某些情景中,数字经常出现,特别是在像表格这样的半结构化数据中。但目前采用变压器语言模型的丰富数量任务的方法放弃或丢失了一些算术信息----例如,将数字破碎成子字符号----这导致许多与数字有关的错误。在本文件中,我们提议LUNA框架,改进变压器语言模型的数字推理和计算能力。在 NumTok 和 NumBed 的插件中,LUNA 代表了每个数字, 特别是在像表那样的半结构化数据中。但是,目前采用以变压器为基础的变压器模型(ROPERTA、BERTBERT) 经常出现数字, 包括回归损失和模型蒸馏,LUNA将数字和词汇嵌入的间隔间隔断。根据我们的知识,这是将算能力明确引入语言模型使用数字 Plugins Plugins。除了评估玩具任务中的微模型,我们还评估三种大型变压变压模型(ROTA、BERTERQ、TABERAT1、TA+TA、SLA的升级的SALA、SALA、SALA、SALQ、SA的升级的SA、SUA的升级的升级式、升级式、TA、TA的SA、升级的SA、升级的SOVA、升级式的升级式、升级式、TA、TA、TA、升级式、升级的SVA、升级的SVA、TA、TA、TA、升级式、升级的SVA、升级的SVA、升级的S-Q、升级的S-Q、升级的SVA、升级的SVA、升级的SVA、升级的SVA-Q、升级的SVA、升级的SVA、升级的SVA、升级式式式式、升级的SA、升级的SALQ、升级的SA、升级的SA、升级的SALA、升级的SA、升级的SA、升级式、升级的SA、升级的SA、升级的SALA、升级的SA、</s>