Bounds on f-Divergences between Distributions within Generalized Quasi-$\varepsilon$-Neighborhood

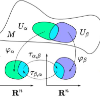
A general reverse Pinsker's inequality is derived to give an upper bound on f-divergences in terms of total variational distance when two distributions are close measured under our proposed generalized local information geometry framework. In addition, relationships between two f-divergences equipped with functions that are third order differentiable are established in terms of the lower and upper bounds of their ratio, when the underlying distributions are within a generalized quasi-$\varepsilon$-neighborhood.