Model hierarchies and higher-order discretisation of time-dependent thin-film free boundary problems with dynamic contact angle

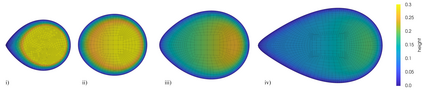
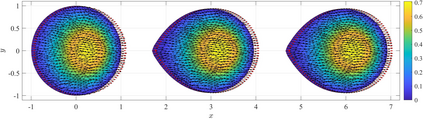
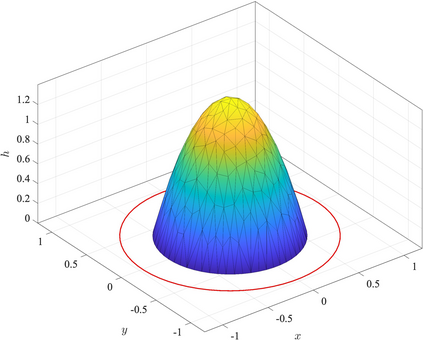
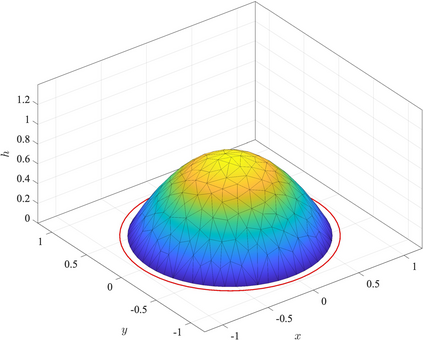
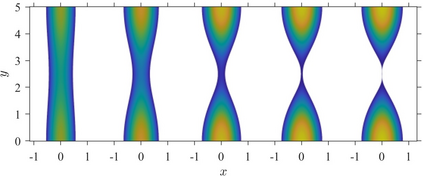
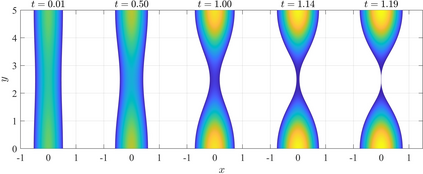
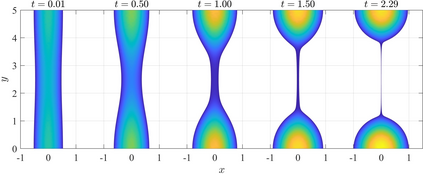
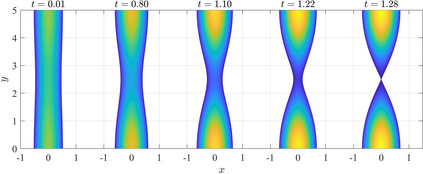
We present a mathematical and numerical framework for thin-film fluid flows over planar surfaces including dynamic contact angles. In particular, we provide algorithmic details and an implementation of higher-order spatial and temporal discretisation of the underlying free boundary problem using the finite element method. The corresponding partial differential equation is based on a thermodynamic consistent energetic variational formulation of the problem using the free energy and viscous dissipation in the bulk, on the surface, and at the moving contact line. Model hierarchies for limits of strong and weak contact line dissipation are established, implemented and studied. We analyze the performance of the numerical algorithm and investigate the impact of the dynamic contact angle on the evolution of two benchmark problems: gravity-driven sliding droplets and the instability of a ridge.