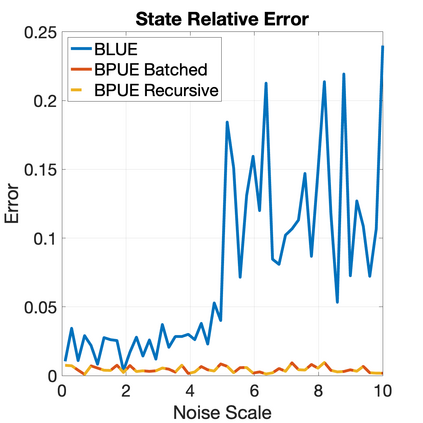
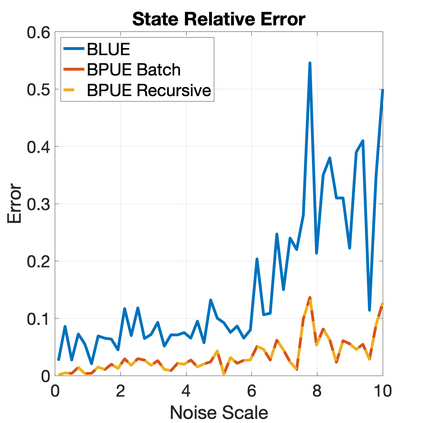
This paper develops a new filtering approach for state estimation in polynomial systems corrupted by arbitrary noise, which commonly arise in robotics. We first consider a batch setup where we perform state estimation using all data collected from the initial to the current time. We formulate the batch state estimation problem as a Polynomial Optimization Problem (POP) and relax the assumption of Gaussian noise by specifying a finite number of moments of the noise. We solve the resulting POP using a moment relaxation and prove that under suitable conditions on the rank of the relaxation, (i) we can extract a provably optimal estimate from the moment relaxation, and (ii) we can obtain a belief representation from the dual (sum-of-squares) relaxation. We then turn our attention to the filtering setup and apply similar insights to develop a GMKF for recursive state estimation in polynomial systems with arbitrary noise. The GMKF formulates the prediction and update steps as POPs and solves them using moment relaxations, carrying over a possibly non-Gaussian belief. In the linear-Gaussian case, GMKF reduces to the standard Kalman Filter. We demonstrate that GMKF performs well under highly non-Gaussian noise and outperforms common alternatives, including the Extended and Unscented Kalman Filter, and their variants on matrix Lie group.
翻译:暂无翻译