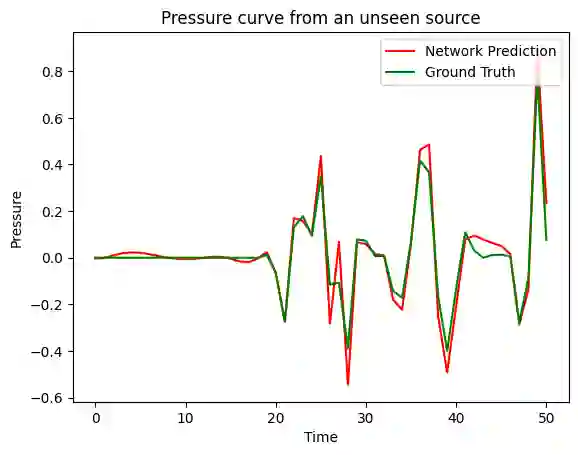
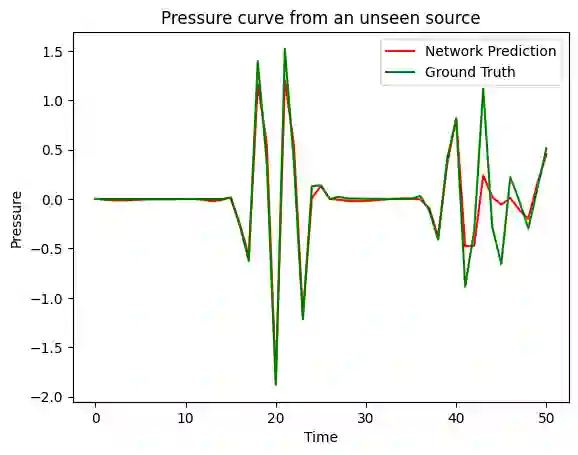
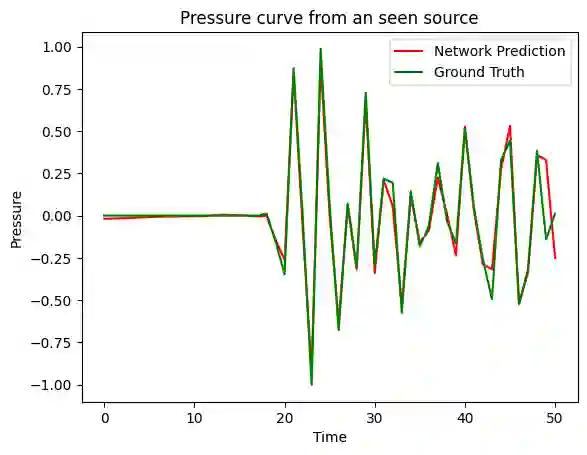
Neural networks have become a powerful tool as surrogate models to provide numerical solutions for scientific problems with increased computational efficiency. This efficiency can be advantageous for numerically challenging problems where time to solution is important or when evaluation of many similar analysis scenarios is required. One particular area of scientific interest is the setting of inverse problems, where one knows the forward dynamics of a system are described by a partial differential equation and the task is to infer properties of the system given (potentially noisy) observations of these dynamics. We consider the inverse problem of inferring the location of a wave source on a square domain, given a noisy solution to the 2-D acoustic wave equation. Under the assumption of Gaussian noise, a likelihood function for source location can be formulated, which requires one forward simulation of the system per evaluation. Using a standard neural network as a surrogate model makes it computationally feasible to evaluate this likelihood several times, and so Markov Chain Monte Carlo methods can be used to evaluate the posterior distribution of the source location. We demonstrate that this method can accurately infer source-locations from noisy data.
翻译:暂无翻译