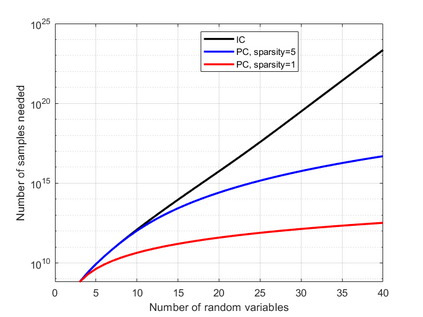
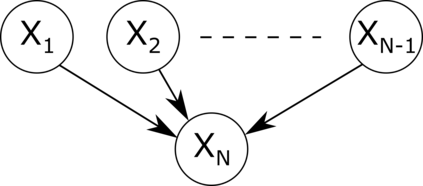
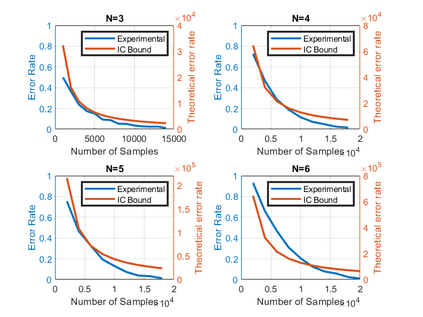
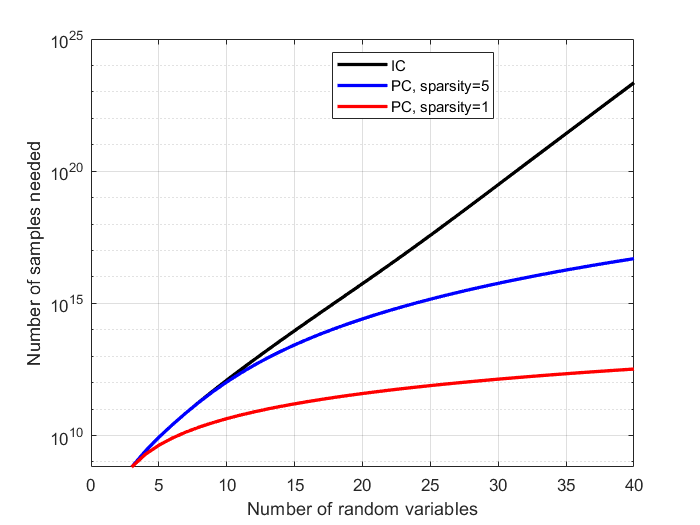
Causal discovery methods seek to identify causal relations between random variables from purely observational data, as opposed to actively collected experimental data where an experimenter intervenes on a subset of correlates. One of the seminal works in this area is the Inferred Causation algorithm, which guarantees successful causal discovery under the assumption of a conditional independence (CI) oracle: an oracle that can states whether two random variables are conditionally independent given another set of random variables. Practical implementations of this algorithm incorporate statistical tests for conditional independence, in place of a CI oracle. In this paper, we analyze the sample complexity of causal discovery algorithms without a CI oracle: given a certain level of confidence, how many data points are needed for a causal discovery algorithm to identify a causal structure? Furthermore, our methods allow us to quantify the value of domain expertise in terms of data samples. Finally, we demonstrate the accuracy of these sample rates with numerical examples, and quantify the benefits of sparsity priors and known causal directions.
翻译:与积极收集的实验数据相比,从纯粹观测数据中随机变量与积极收集的实验数据之间有因果关系,实验者在其中干预一个相关子群。该领域的开创性工作之一是 " 推断性因果关系算法 ",它保证在有条件的独立(CI)甲骨文假设下成功发现因果:一个神器,它可以说明两个随机变量是否有条件地独立,并给出另一组随机变量。这一算法的实际应用包括有条件独立统计测试,而不是CI 甲骨文。在本文中,我们分析了因果发现算法的抽样复杂性,而没有CI 甲骨文:根据某种程度的自信,为了确定因果结构,需要多少数据点?此外,我们的方法使我们能够用数字示例来量化领域专门知识的价值。最后,我们用数字示例来显示这些抽样率的准确性,并量化紧张性前期和已知因果方向的好处。