An Algorithm for the Discovery of Independence from Data

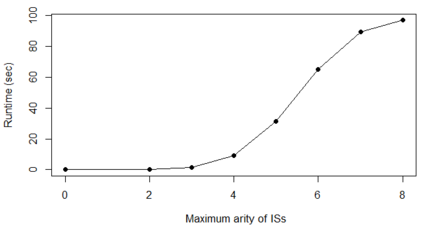
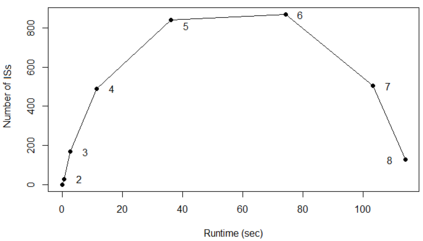
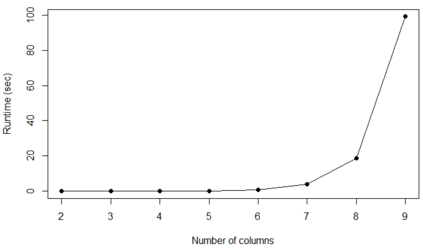
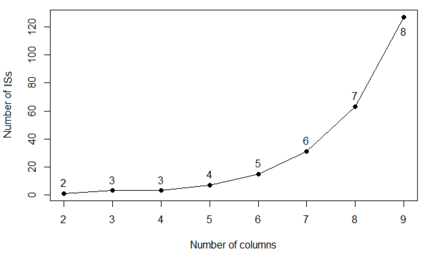
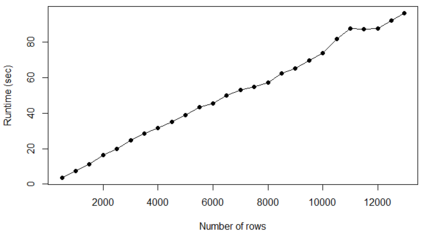
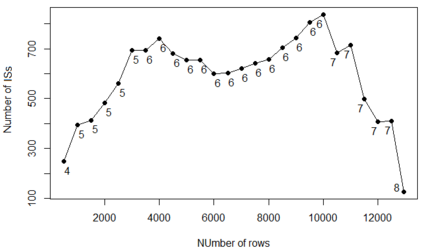
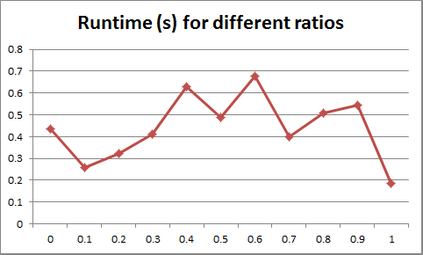
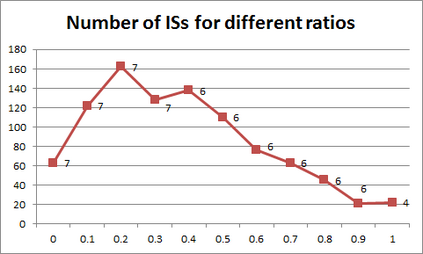
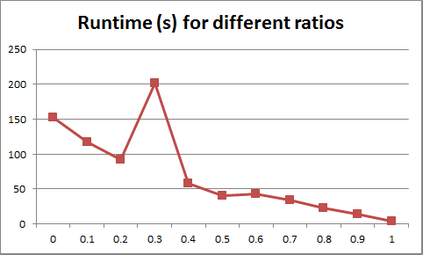
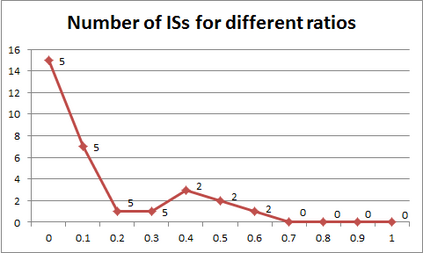
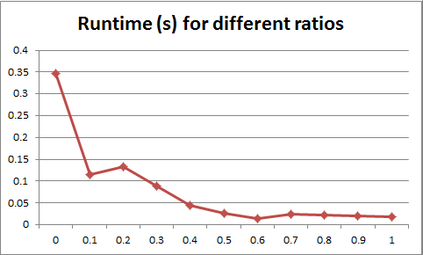
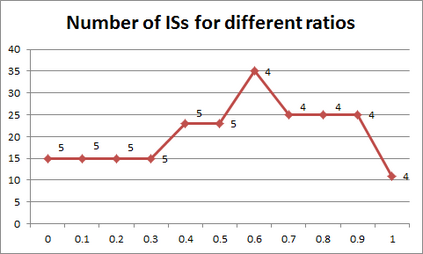
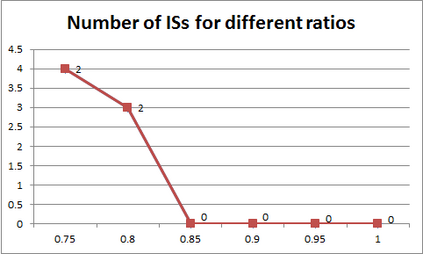
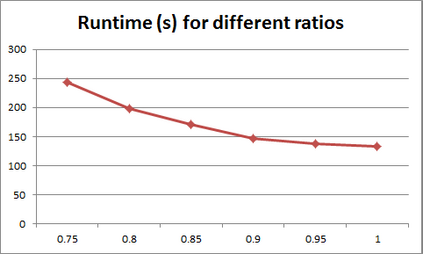
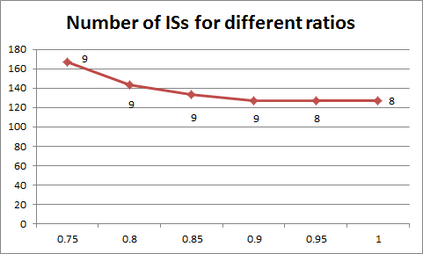
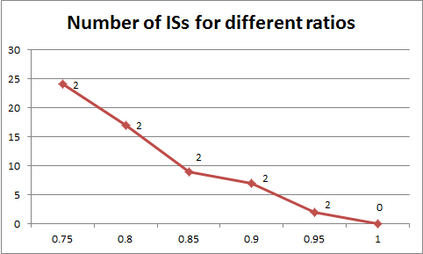
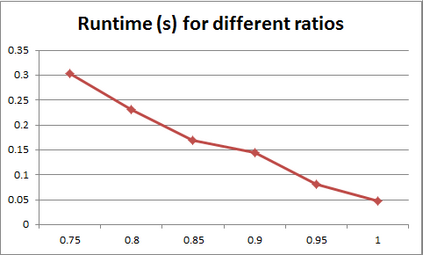
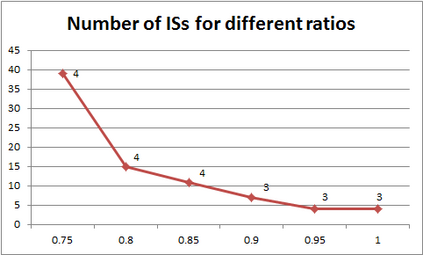
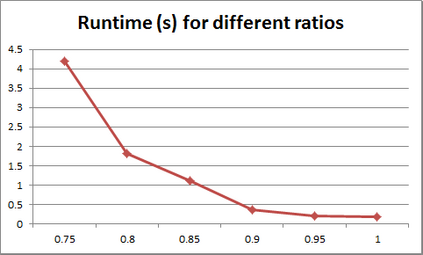
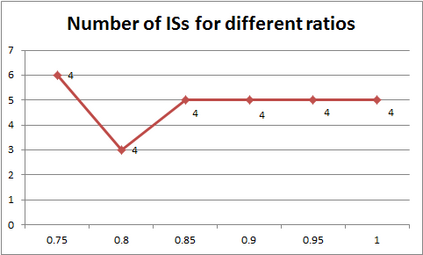
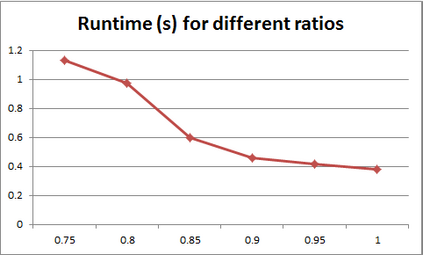
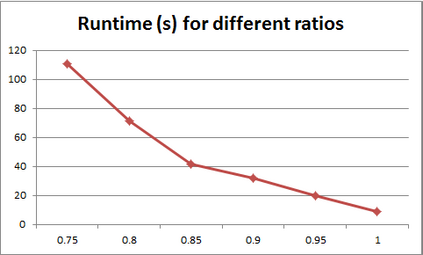
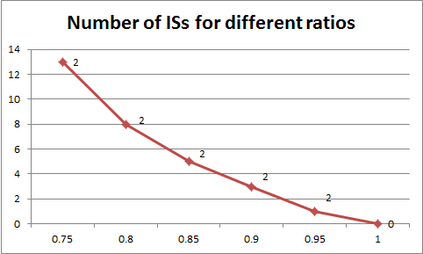
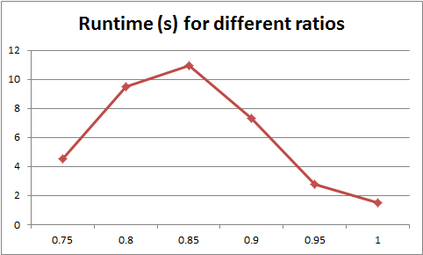
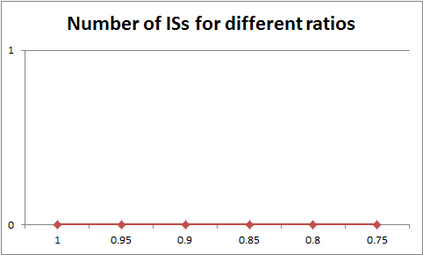
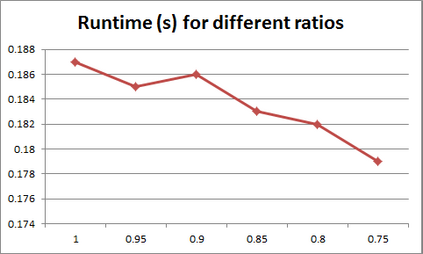
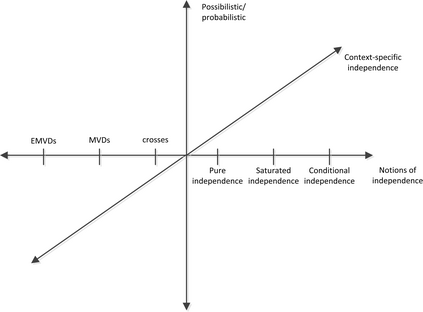
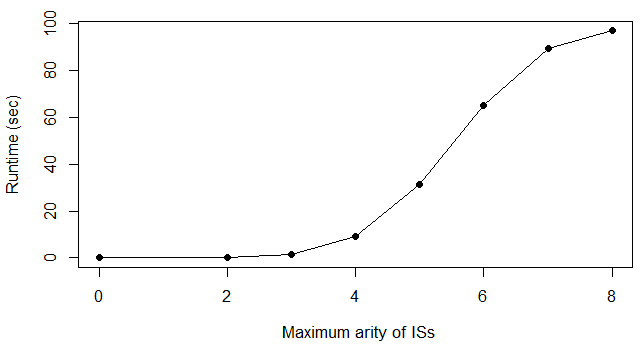
For years, independence has been considered as an important concept in many disciplines. Nevertheless, we present the first research that investigates the discovery problem of independence in data. In its arguably simplest form, independence is a statement between two sets of columns expressing that for every two rows in a table there is also a row in the table that coincides with the first row on the first set of columns and with the second row on the second set of columns. We show that the problem of deciding whether there is an independence statement that holds on a given table is not only NP-complete but $W[3]$-complete in its arguably most natural parameter, namely its arity. We establish the first algorithm to discover all independence statement that hold on a given table. We illustrate in experiments with benchmark data that our algorithm performs well within the limits established by our hardness results. In practice, it is often useful to determine the ratio with which independence statements hold on a given table. For that purpose, we show that our treatment of independence and the design of our algorithm enables us to extend our findings to approximate independence. In our final experiments, we provide some insight into the trade-off between run time and the approximation ratio. Naturally, the smaller the ratio, the more approximate independence statements hold, and the more time it takes to discover all of them. While this research establishes first insight into the computational properties of discovering independence from data, we hope to initiate research into more sophisticated notions of independence, including embedded multivalued dependencies, as well as their context-specific and probabilistic variants.