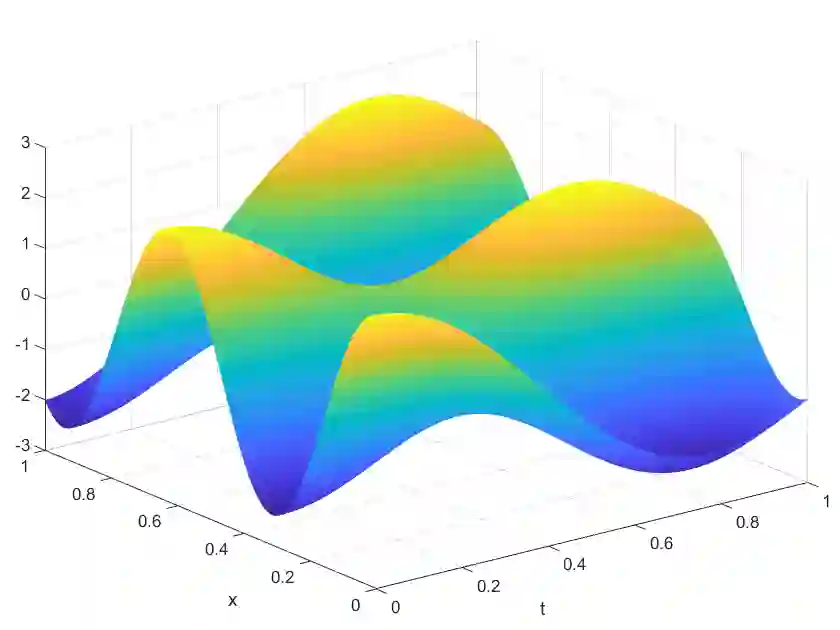
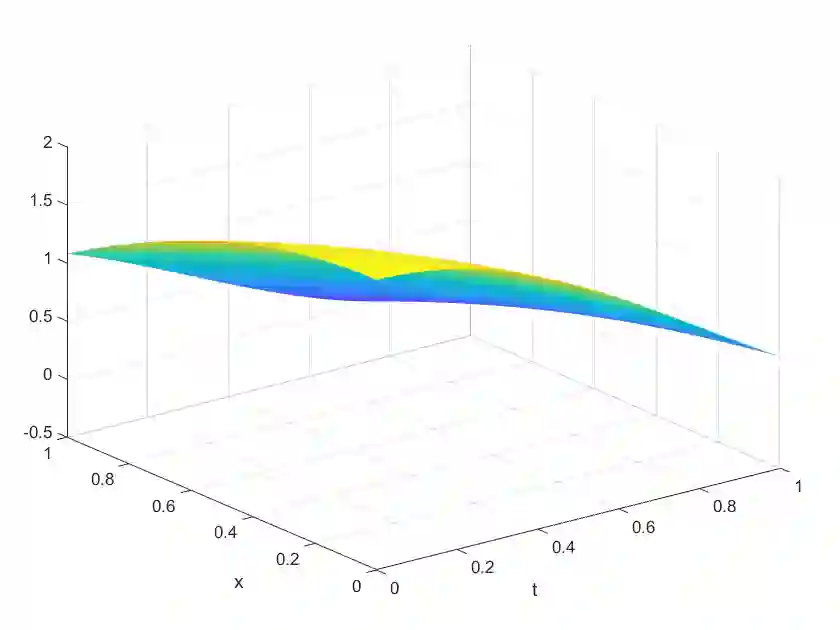
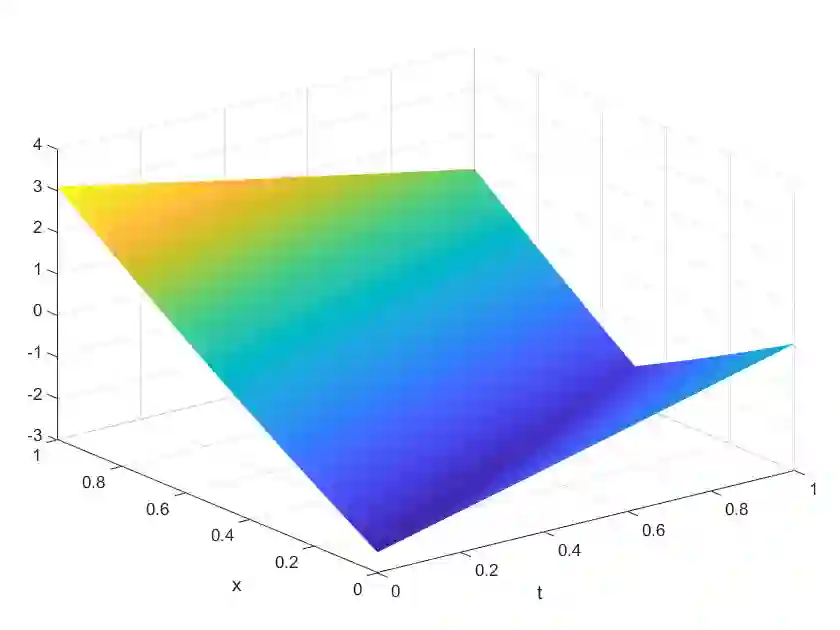
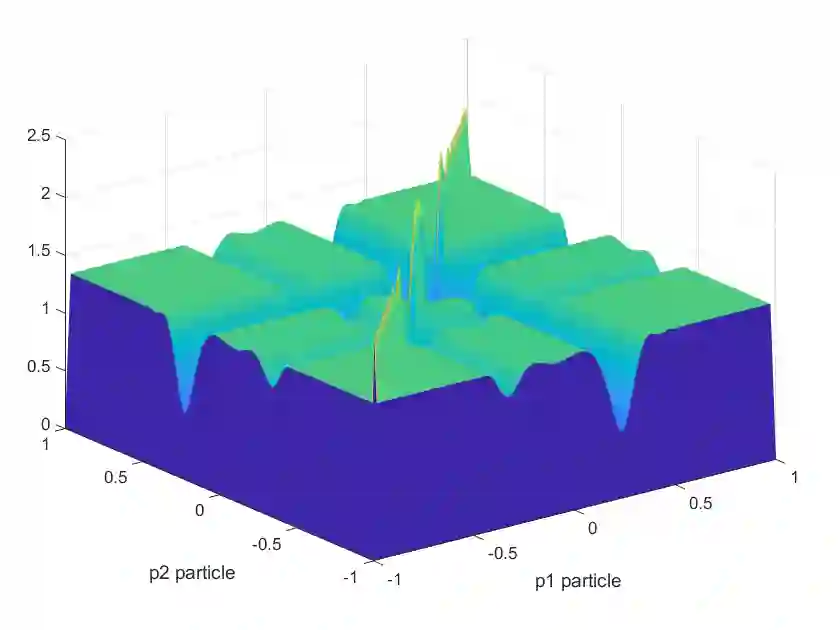
We consider approximations formed by the sum of a linear combination of given functions enhanced by ridge functions -- a Linear/Ridge expansion. For an explicitly or implicitly given function, we reformulate finding a best Linear/Ridge expansion in terms of an optimization problem. We introduce a particle grid algorithm for its solution. Several numerical results underline the flexibility, robustness and efficiency of the algorithm. One particular source of motivation is model reduction of parameterized transport or wave equations. We show that the particle grid algorithm is able to produce a Linear/Ridge expansion as an efficient nonlinear model reduction.
翻译:我们认为,通过由脊柱函数增强的给定函数的线性组合总和所形成的近似值 -- -- 线性/Ridge扩展。对于一个明示或隐含的函数,我们重塑了在优化问题方面找到最佳线性/Ridge扩展值的方法。我们引入了粒子网格算法来解决这个问题。若干数字结果强调了算法的灵活性、稳健性和效率。动力的一个具体来源是参数化运输或波形方程式的模型减少。我们显示,粒子网格算法能够产生线性/Ridge扩展值,作为有效的非线性模型减少值。