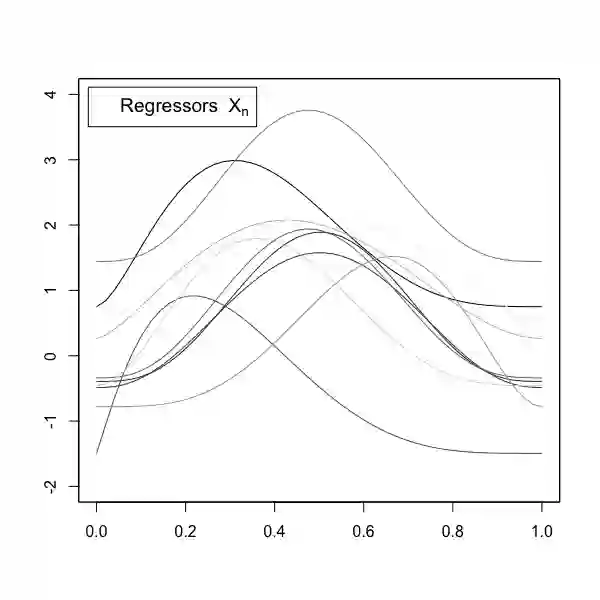
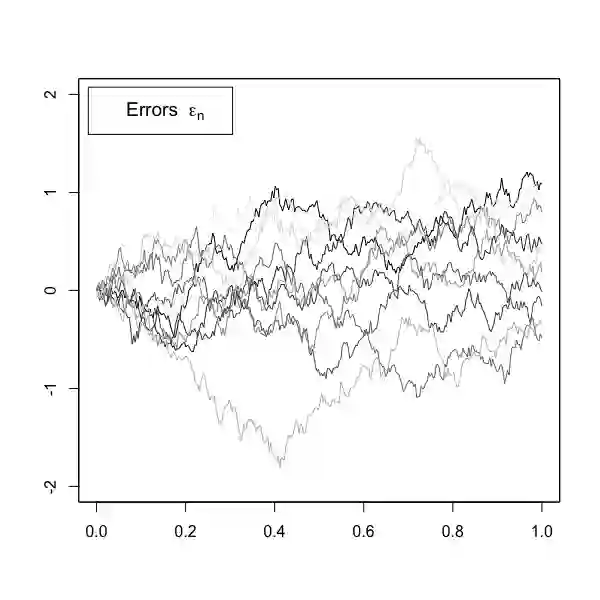
In this paper we consider the linear regression model $Y =S X+\varepsilon $ with functional regressors and responses. We develop new inference tools to quantify deviations of the true slope $S$ from a hypothesized operator $S_0$ with respect to the Hilbert--Schmidt norm $\| S- S_0\|^2$, as well as the prediction error $\mathbb{E} \| S X - S_0 X \|^2$. Our analysis is applicable to functional time series and based on asymptotically pivotal statistics. This makes it particularly user friendly, because it avoids the choice of tuning parameters inherent in long-run variance estimation or bootstrap of dependent data. We also discuss two sample problems as well as change point detection. Finite sample properties are investigated by means of a simulation study.\\ Mathematically our approach is based on a sequential version of the popular spectral cut-off estimator $\hat S_N$ for $S$. It is well-known that the $L^2$-minimax rates in the functional regression model, both in estimation and prediction, are substantially slower than $1/\sqrt{N}$ (where $N$ denotes the sample size) and that standard estimators for $S$ do not converge weakly to non-degenerate limits. However, we demonstrate that simple plug-in estimators - such as $\| \hat S_N - S_0 \|^2$ for $\| S - S_0 \|^2$ - are $\sqrt{N}$-consistent and its sequential versions satisfy weak invariance principles. These results are based on the smoothing effect of $L^2$-norms and established by a new proof-technique, the {\it smoothness shift}, which has potential applications in other statistical inverse problems.
翻译:在本文中,我们考虑了线性回归模型 $Y = S X_0 X = 2美元。 我们的分析适用于功能时间序列, 并且基于非同步枢纽统计数据。 这让用户特别友好, 因为它避免选择长期差异估计或依赖数据的靴套中固有的调值参数。 我们还讨论两个样本问题以及更改点检测。 通过模拟研究来调查精度样本属性。\\ 从数学角度讲, 我们的方法是以流行的光谱切价估量 $ - S_0 X =2 =2 $。 我们的分析适用于功能时间序列, 并且基于静态关键统计数据序列。 S_ =2 N= 美元 。 我们非常清楚知道, 在长期差异估测或依赖数据的靴套件中, 基底值的调值值和基底值值都存在新问题, 基底值的S_ ====美元。