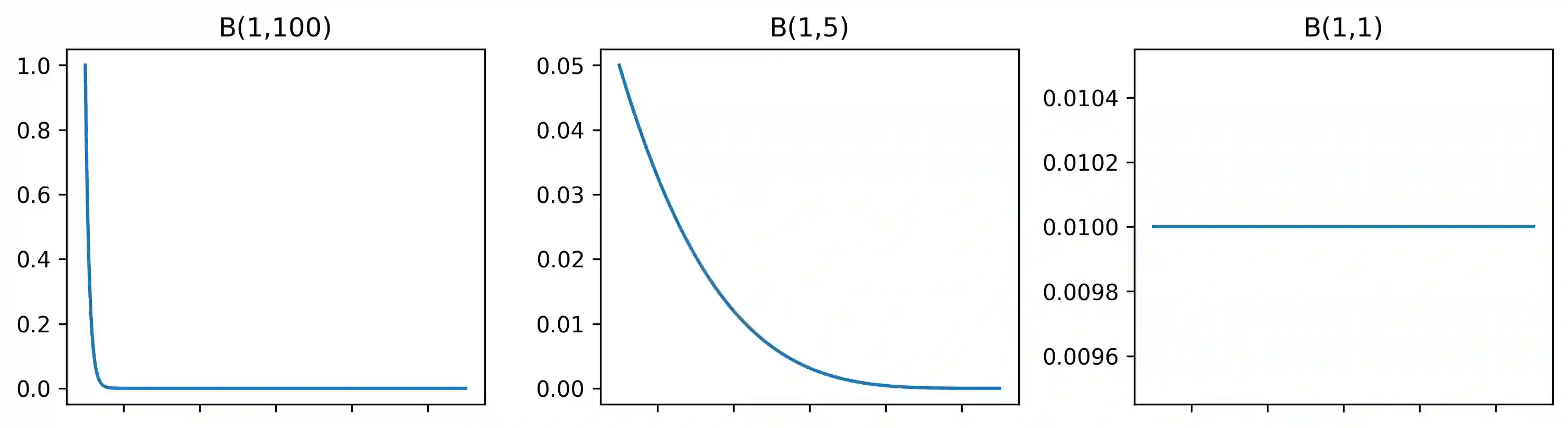
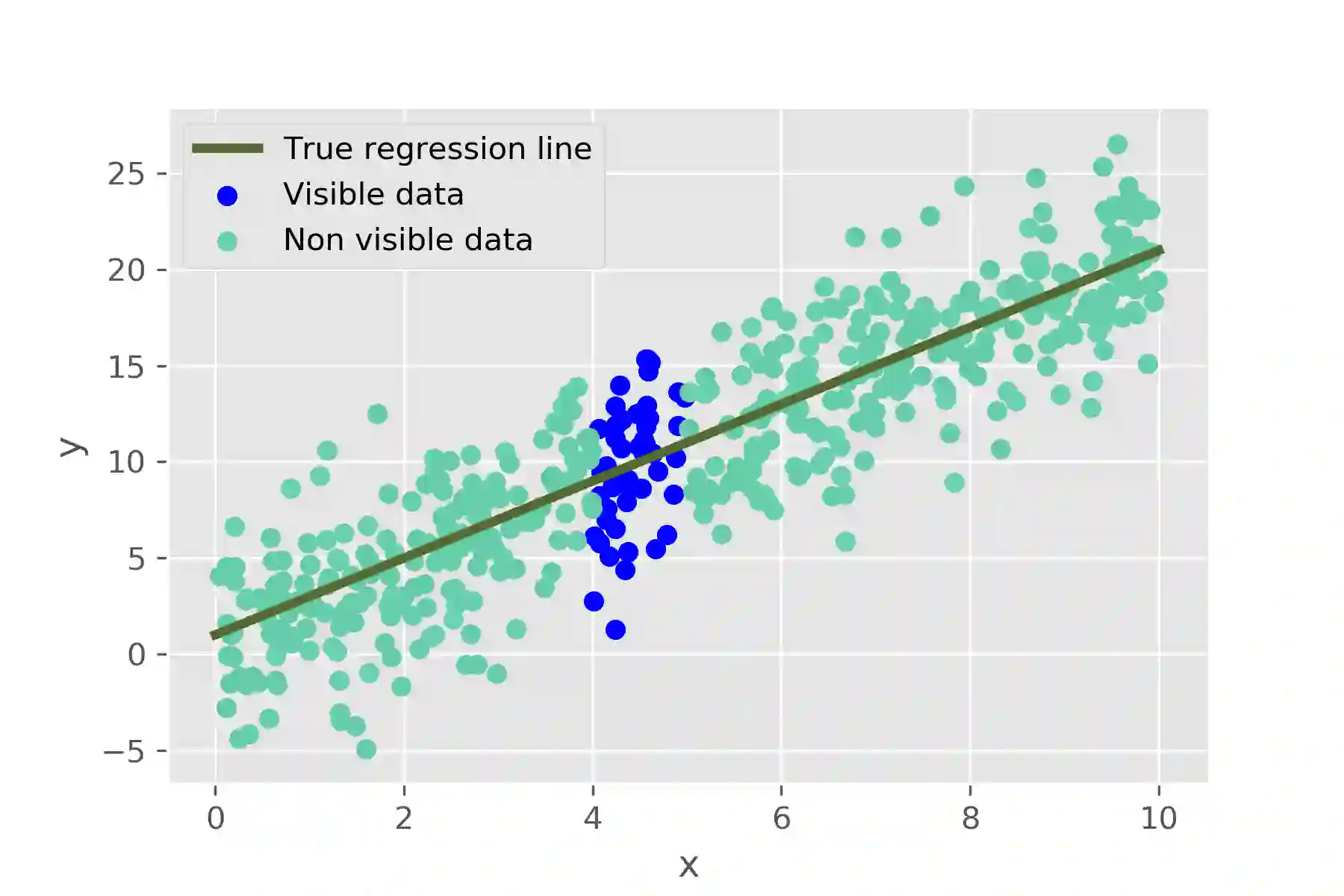
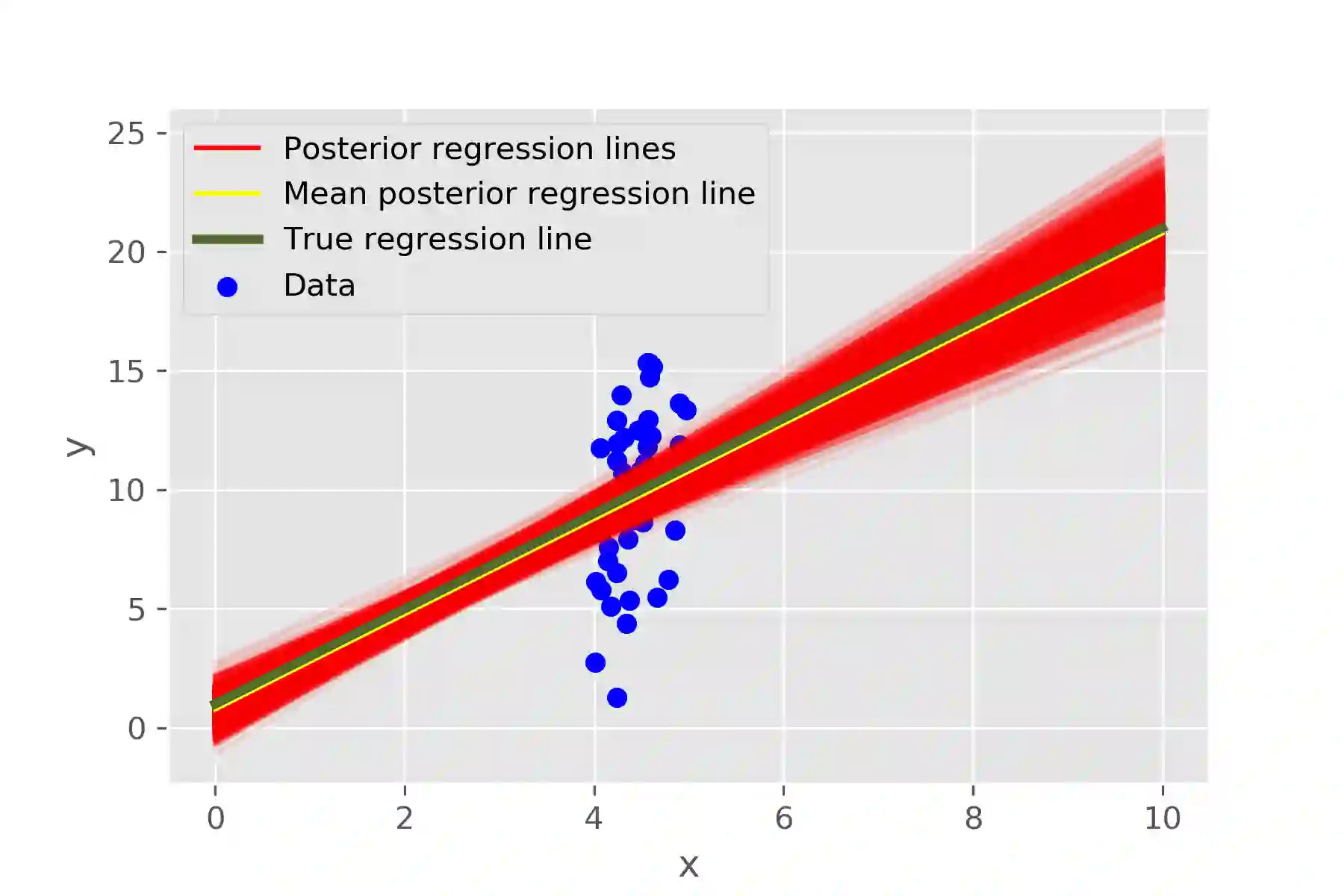
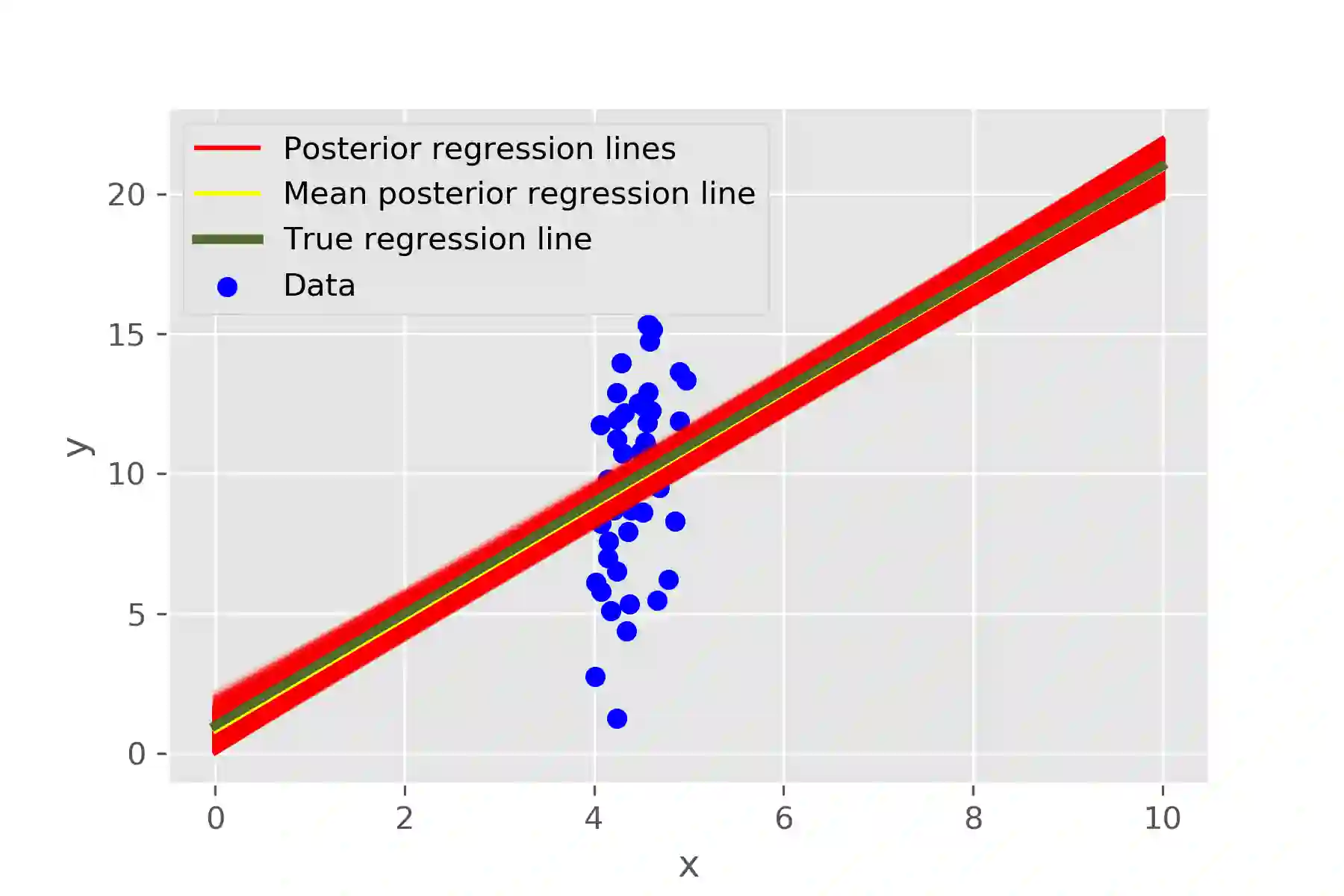
We introduce a novel rule-based approach for handling regression problems. The new methodology carries elements from two frameworks: (i) it provides information about the uncertainty of the parameters of interest using Bayesian inference, and (ii) it allows the incorporation of expert knowledge through rule-based systems. The blending of those two different frameworks can be particularly beneficial for various domains (e.g. engineering), where, even though the significance of uncertainty quantification motivates a Bayesian approach, there is no simple way to incorporate researcher intuition into the model. We validate our models by applying them to synthetic applications: a simple linear regression problem and two more complex structures based on partial differential equations. Finally, we review the advantages of our methodology, which include the simplicity of the implementation, the uncertainty reduction due to the added information and, in some occasions, the derivation of better point predictions, and we address limitations, mainly from the computational complexity perspective, such as the difficulty in choosing an appropriate algorithm and the added computational burden.
翻译:新方法包含两个框架的内容:(一) 它提供了使用巴耶斯推理法的利息参数不确定性的信息,以及(二) 它允许通过基于规则的系统纳入专家知识。 将这两个不同的框架混合起来,对各个领域(例如工程)特别有利,尽管不确定性的量化意义促使采用巴耶斯方法,但没有简单的方法将研究者的直觉纳入模型。我们通过将模型应用于合成应用来验证我们的模型:一个简单的线性回归问题和基于部分差异方程式的两种更为复杂的结构。 最后,我们审查我们的方法的优点,其中包括执行的简单性、由于增加的信息而减少的不确定性,以及在某些情况下,改进点预测的衍生,我们主要从计算复杂性的角度处理局限性,例如选择适当的算法的困难和增加的计算负担。