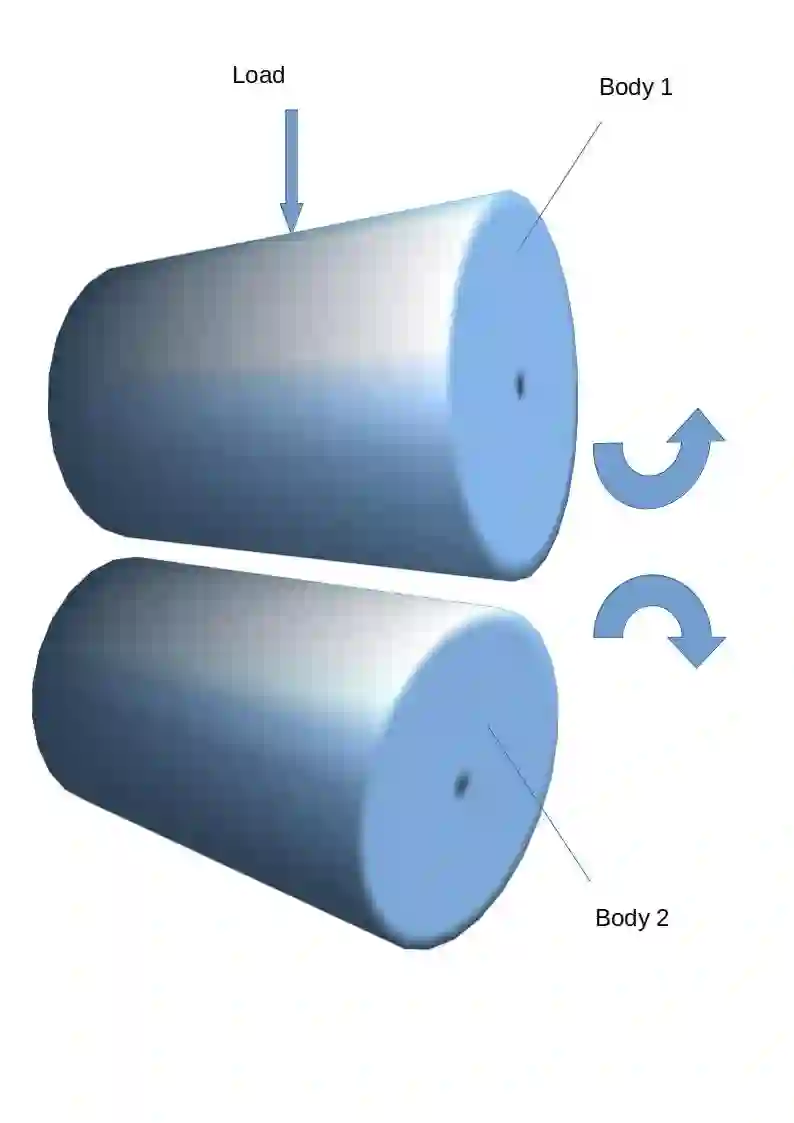
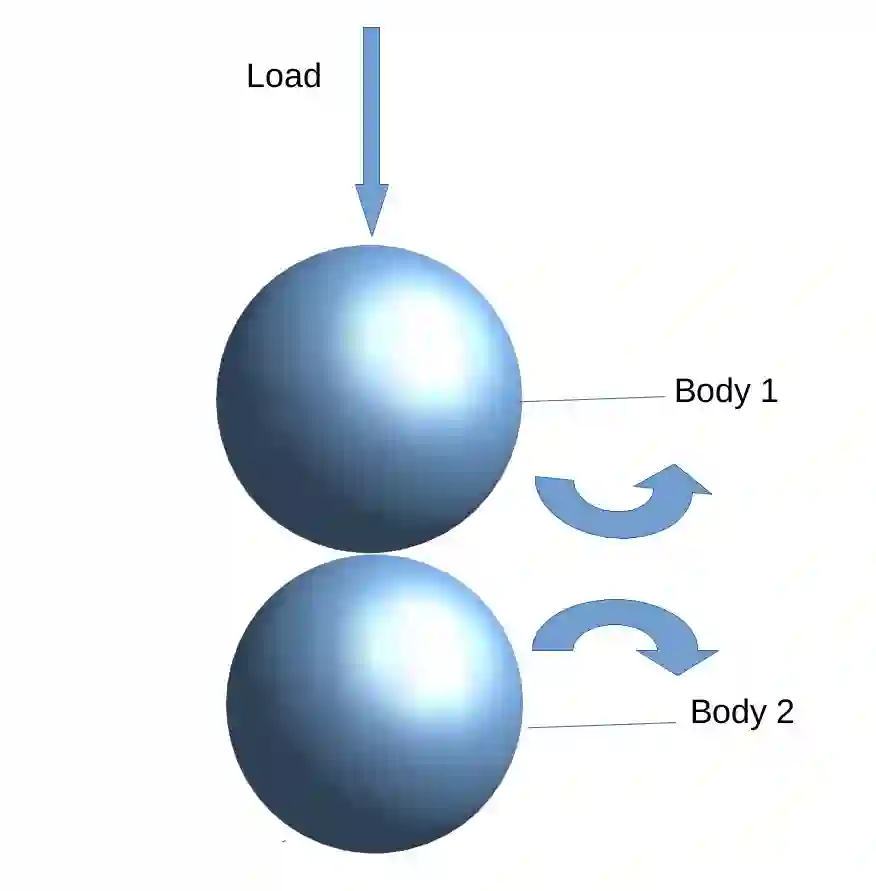
In the present study, an interior-exterior penalty discontinuous Galerkin finite element method (DG-FEM) is analysed for solving Elastohydrodynamic lubrication (EHL) line and point contact problems. The existence of discrete penalized solution is examined using Brouwer's fixed point theorem. Furthermore, the uniqueness of solution is proved using Lipschitz continuity of the discrete solution map under light load parameter assumptions. A priori error estimates are achieved in $L^{2}$ and $H^{1}$ norms which are shown to be optimal in mesh size $h$ and suboptimal in polynomial degree $p$. The validity of theoretical findings are confirmed through series of numerical experiments.
翻译:在本研究中,分析了一种内部外处刑不连续加列尔金限定元素法(DG-FEM),以解决 Elasto氢力润滑剂(EHL)线和点接触问题;利用Brouwer的固定点理论来审查是否存在受制裁的离散溶液;此外,使用Lipschitz的离散溶液图在轻负荷参数假设下的连续性证明了溶液的独特性;用$L ⁇ 2}美元和$H1}美元得出了先验误差估计数,这些估计数在网状尺寸上为$h$,在多元度上为$p$;通过一系列数字实验证实了理论结论的有效性。