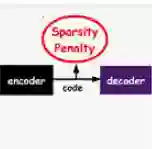
Deep latent generative models have attracted increasing attention due to the capacity of combining the strengths of deep learning and probabilistic models in an elegant way. The data representations learned with the models are often continuous and dense. However in many applications, sparse representations are expected, such as learning sparse high dimensional embedding of data in an unsupervised setting, and learning multi-labels from thousands of candidate tags in a supervised setting. In some scenarios, there could be further restriction on degree of sparsity: the number of non-zero features of a representation cannot be larger than a pre-defined threshold $L_0$. In this paper we propose a sparse deep latent generative model SDLGM to explicitly model degree of sparsity and thus enable to learn the sparse structure of the data with the quantified sparsity constraint. The resulting sparsity of a representation is not fixed, but fits to the observation itself under the pre-defined restriction. In particular, we introduce to each observation $i$ an auxiliary random variable $L_i$, which models the sparsity of its representation. The sparse representations are then generated with a two-step sampling process via two Gumbel-Softmax distributions. For inference and learning, we develop an amortized variational method based on MC gradient estimator. The resulting sparse representations are differentiable with backpropagation. The experimental evaluation on multiple datasets for unsupervised and supervised learning problems shows the benefits of the proposed method.
翻译:----
深度潜在生成模型因将深度学习和概率模型的优势以简洁而优美的方式相结合而受到越来越多的关注。模型学习的数据表示通常是连续和密集的。然而,在许多应用中,期望的表示是稀疏的,例如在无监督设置中学习数据的稀疏高维嵌入,以及在监督设置中从数千个候选标签中学习多标签。在某些情况下,可能会对稀疏程度施加进一步的限制:表示的非零特征数不能超过预定义阈值L0。本文提出稀疏深潜在生成模型SDLGM,以显式地建模稀疏度从而实现在量化稀疏约束下学习数据的稀疏结构。表示的结果不是固定的,而是适应于预定义限制下的观察本身。特别地,我们为每个观察添加一个辅助随机变量Li,用于对其表示的稀疏度进行建模。然后通过两个Gumbel-Softmax分布的两步抽样过程生成稀疏表示。对于推断和学习,我们开发了基于MC梯度估计器的估计变分方法。稀疏表示是可微分的,可以通过反向传播来处理。在无监督和有监督学习问题上,对多个数据集进行的实验评估显示出了所提出方法的优越性。