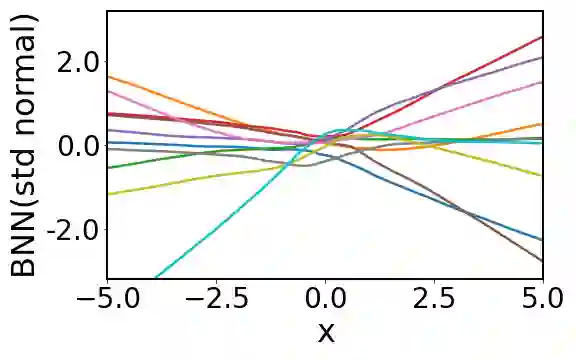
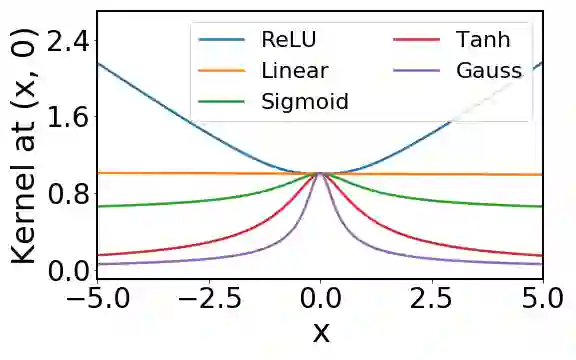
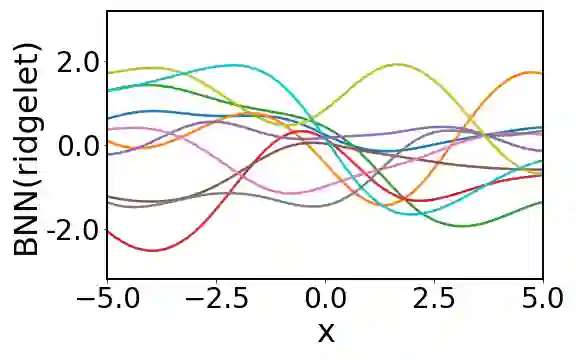
Bayesian neural networks attempt to combine the strong predictive performance of neural networks with formal quantification of uncertainty associated with the predictive output in the Bayesian framework. However, it remains unclear how to endow the parameters of the network with a prior distribution that is meaningful when lifted into the output space of the network. A possible solution is proposed that enables the user to posit an appropriate Gaussian process covariance function for the task at hand. Our approach constructs a prior distribution for the parameters of the network, called a ridgelet prior, that approximates the posited Gaussian process in the output space of the network. In contrast to existing work on the connection between neural networks and Gaussian processes, our analysis is non-asymptotic, with finite sample-size error bounds provided. This establishes the universality property that a Bayesian neural network can approximate any Gaussian process whose covariance function is sufficiently regular. Our experimental assessment is limited to a proof-of-concept, where we demonstrate that the ridgelet prior can out-perform an unstructured prior on regression problems for which a suitable Gaussian process prior can be provided.
翻译:Bayesian 神经网络试图将神经网络的强力预测性性能与与Bayesian 框架中预测性产出的不确定性的正式量化结合起来。 但是,仍然不清楚如何将网络参数与网络输出空间提升到网络输出空间时具有实际意义的先前分布相匹配。 提出了一个可能的解决办法, 使用户能够为手头的任务设定一个适当的高斯进程共变函数。 我们的方法为网络参数( 称为前脊椎线)预设高斯进程预设了事先分布, 接近网络输出空间中的假设高斯进程。 与关于神经网络和高斯进程之间连接的现有工作相比, 我们的分析是非被动的, 提供了有限的样本大小错误界限 。 这确立了一个普遍性属性, 即巴伊西亚神经网络可以近似任何常态功能的高斯进程。 我们的实验评估限于一个验证概念, 在那里我们证明, 前高斯 能够超越一个合适的古斯之前的回归进程。