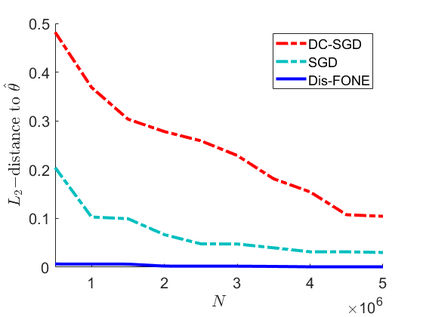
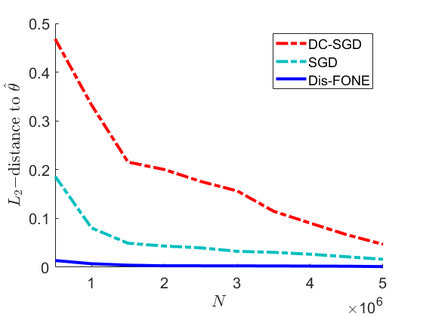
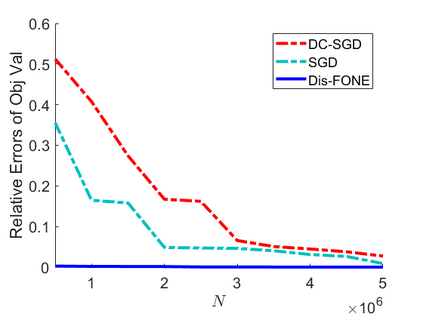
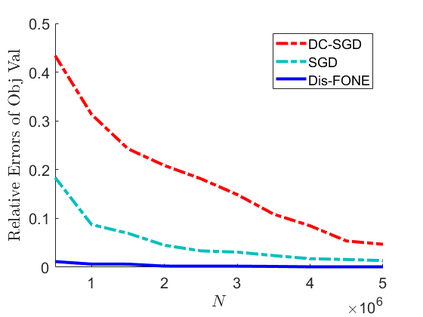
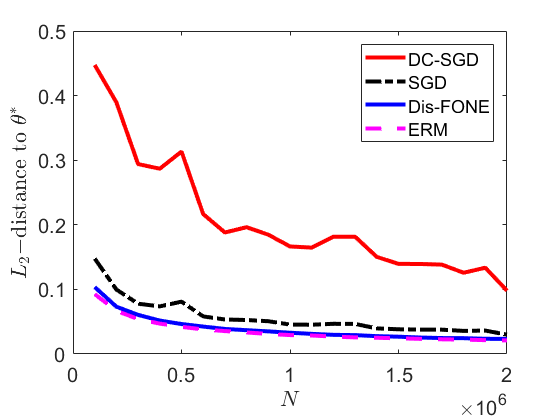
This paper studies distributed estimation and inference for a general statistical problem with a convex loss that could be non-differentiable. For the purpose of efficient computation, we restrict ourselves to stochastic first-order optimization, which enjoys low per-iteration complexity. To motivate the proposed method, we first investigate the theoretical properties of a straightforward Divide-and-Conquer Stochastic Gradient Descent (DC-SGD) approach. Our theory shows that there is a restriction on the number of machines and this restriction becomes more stringent when the dimension $p$ is large. To overcome this limitation, this paper proposes a new multi-round distributed estimation procedure that approximates the Newton step only using stochastic subgradient. The key component in our method is the proposal of a computationally efficient estimator of $\Sigma^{-1} w$, where $\Sigma$ is the population Hessian matrix and $w$ is any given vector. Instead of estimating $\Sigma$ (or $\Sigma^{-1}$) that usually requires the second-order differentiability of the loss, the proposed First-Order Newton-type Estimator (FONE) directly estimates the vector of interest $\Sigma^{-1} w$ as a whole and is applicable to non-differentiable losses. Our estimator also facilitates the inference for the empirical risk minimizer. It turns out that the key term in the limiting covariance has the form of $\Sigma^{-1} w$, which can be estimated by FONE.
翻译:本文的论文研究将估算和推论用于一个一般的统计问题, 其成本损失可能无法区分。 为了高效计算, 我们只提出一个新的多轮分配估算程序, 仅使用随机亚梯度来接近牛顿步骤的一级优化, 这种方法的复杂度较低。 为了激励拟议方法, 我们首先调查一个直接的分化和盘算取渐进源( DC- SGD) 方法的理论性能。 我们的理论显示, 机器的数量是有限制的, 而当尺寸大时, 这一限制会变得更加严格。 为了克服这一限制, 本文建议了一个新的多轮分配估算程序, 只有使用随机次的次度来接近牛顿步骤。 我们的方法中的关键部分是提出一个计算高效的 $\ sigma_-1 w, 美元是人口黑森矩阵, 美元是任何给定矢量。 而不是估计美元( 或 美元=Sigma_ 1} 美元) 通常需要第二阶次的最小度风险度分布, 只能使用随机次的一级 度 度 度 。 牛顿 估计值 方向 方向 。 作为整个方向 的 方向, 的 。 方向 的 和 方向 方向 的 方向 的 轴 的 的 的 的 的 的 也是整个方向 的 的 的 。 。