Continuous-time fully distributed generalized Nash equilibrium seeking for multi-integrator agents

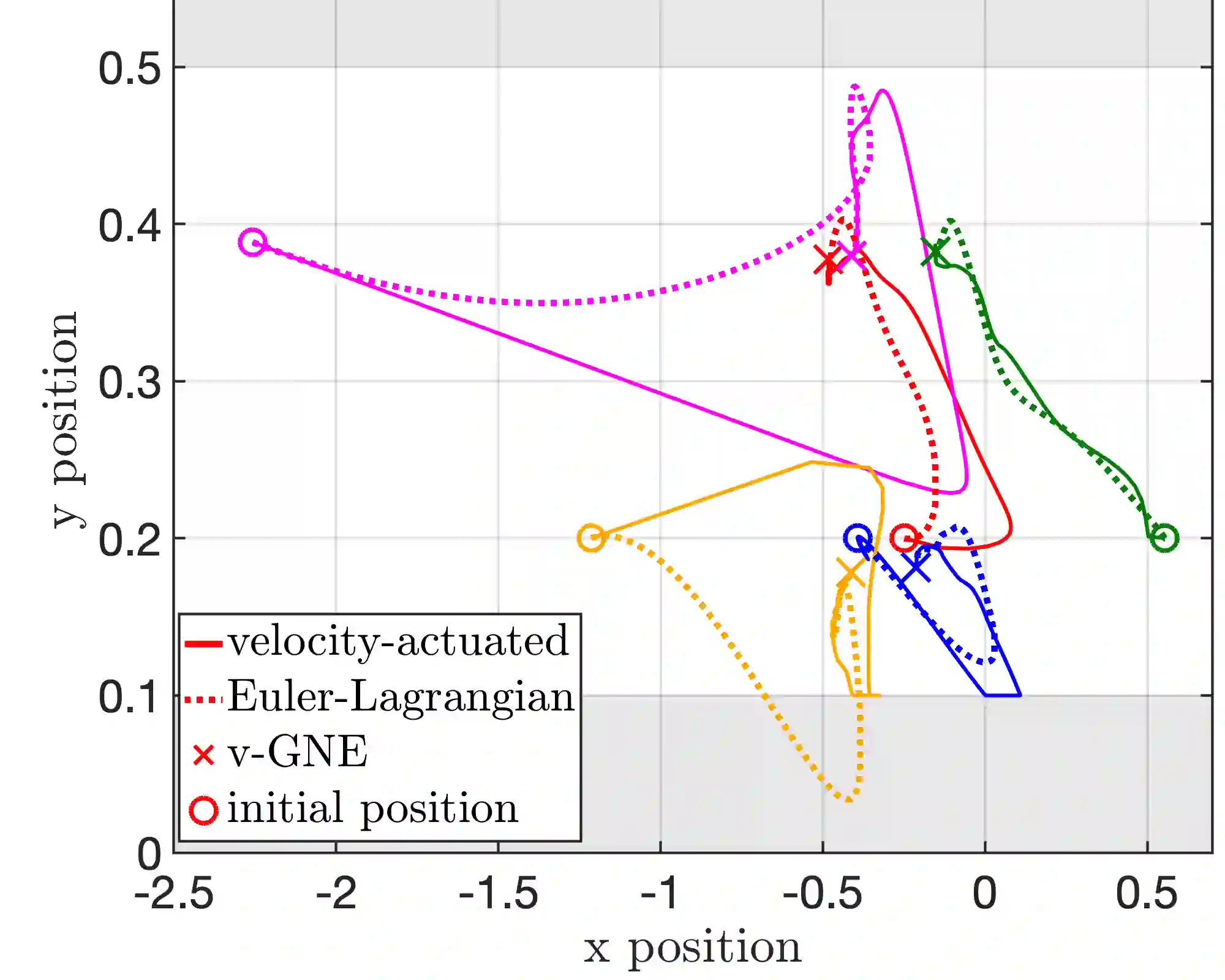
We consider strongly monotone games with convex separable coupling constraints, played by dynamical agents, in a partial-decision information scenario. We start by designing continuous-time fully distributed feedback controllers, based on consensus and primal-dual gradient dynamics, to seek a generalized Nash equilibrium in networks of single-integrator agents. Our first solution adopts a fixed gain, whose choice requires the knowledge of some global parameters of the game. To relax this requirement, we conceive a controller that can be tuned in a completely decentralized fashion, thanks to the use of uncoordinated integral adaptive weights. We further introduce algorithms specifically devised for generalized aggregative games. Finally, we adapt all our control schemes to deal with heterogeneous multi-integrator agents and, in turn, with nonlinear feedback-linearizable dynamical systems. For all the proposed dynamics, we show convergence to a variational equilibrium, by leveraging monotonicity properties and stability theory for projected dynamical systems.