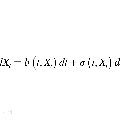Backward Stochastic Differential Equations (BSDEs) have been widely employed in various areas of social and natural sciences, such as the pricing and hedging of financial derivatives, stochastic optimal control problems, optimal stopping problems and gene expression. Most BSDEs cannot be solved analytically and thus numerical methods must be applied to approximate their solutions. There have been a variety of numerical methods proposed over the past few decades as well as many more currently being developed. For the most part, they exist in a complex and scattered manner with each requiring a variety of assumptions and conditions. The aim of the present work is thus to systematically survey various numerical methods for BSDEs, and in particular, compare and categorize them, for further developments and improvements. To achieve this goal, we focus primarily on the core features of each method based on an extensive collection of 333 references: the main assumptions, the numerical algorithm itself, key convergence properties and advantages and disadvantages, to provide an up-to-date coverage of numerical methods for BSDEs, with insightful summaries of each and a useful comparison and categorization.
翻译:反向随机微分方程(BSDEs)在社会和自然科学的各个领域广泛应用,例如金融衍生品的定价和对冲、随机最优控制问题、最优停时问题以及基因表达。大多数BSDE不能解析地求解,因此需要应用数值方法来近似求解。在过去几十年中,已经提出了各种数值方法,并且目前正在开发更多数值方法。大部分方法都存在着复杂和分散的情况,每种方法都需要各种假设和条件。因此,本文的目的是对BSDE的各种数值方法进行系统综述,特别是进行对比和分类,以促进进一步的发展和改进。为实现这一目标,本文主要关注每种方法的核心特点,基于广泛的333个参考文献:主要假设,数值算法本身,主要的收敛性质以及优缺点,为反向随机微分方程的数值方法提供最新报导,概述了每种方法的有益比较和分类。