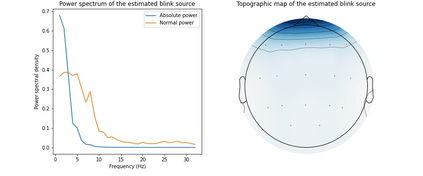
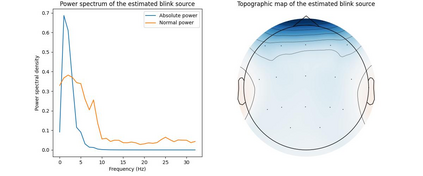
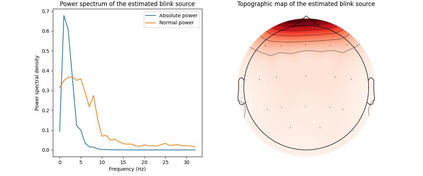
A family of symmetric matrices $A_1,\ldots, A_d$ is SDC (simultaneous diagonalization by congruence) if there is an invertible matrix $X$ such that every $X^T A_k X$ is diagonal. In this work, a novel randomized SDC (RSDC) algorithm is proposed that reduces SDC to a generalized eigenvalue problem by considering two (random) linear combinations of the family. We establish exact recovery: RSDC achieves diagonalization with probability $1$ if the family is exactly SDC. Under a mild regularity assumption, robust recovery is also established: Given a family that is $\epsilon$-close to SDC then RSDC diagonalizes, with high probability, the family up to an error of norm $\mathcal{O}(\epsilon)$. Under a positive definiteness assumption, which often holds in applications, stronger results are established, including a bound on the condition number of the transformation matrix. For practical use, we suggest to combine RSDC with an optimization algorithm. The performance of the resulting method is verified for synthetic data, image separation and EEG analysis tasks. It turns out that our newly developed method outperforms existing optimization-based methods in terms of efficiency while achieving a comparable level of accuracy.
翻译:暂无翻译