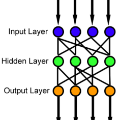
Several neural network approaches for solving differential equations employ trial solutions with a feedforward neural network. There are different means to incorporate the trial solution in the construction, for instance one may include them directly in the cost function. Used within the corresponding neural network, the trial solutions define the so-called neural form. Such neural forms represent general, flexible tools by which one may solve various differential equations. In this article we consider time-dependent initial value problems, which require to set up the neural form framework adequately. The neural forms presented up to now in the literature for such a setting can be considered as first order polynomials. In this work we propose to extend the polynomial order of the neural forms. The novel collocation-type construction includes several feedforward neural networks, one for each order. Additionally, we propose the fragmentation of the computational domain into subdomains. The neural forms are solved on each subdomain, whereas the interfacing grid points overlap in order to provide initial values over the whole fragmentation. We illustrate in experiments that the combination of collocation neural forms of higher order and the domain fragmentation allows to solve initial value problems over large domains with high accuracy and reliability.
翻译:用于解决差异方程式的神经网络方法有几种神经网络方法, 采用试验方法来解决差异方程式, 并配有饲料向外神经网络。 将试验方程式纳入构造中有不同的方法, 例如, 可能直接将试验方程式纳入成本函数。 试验方程式在相应的神经网络中使用, 试验方程式定义所谓的神经形式。 这些神经形式代表了一般的、 灵活的工具, 从而可以解决各种差异方程式。 本条我们考虑的是, 需要适当建立神经形式框架的初始值问题。 文献中目前为这种设置提供的神经形式可以被视为第一个顺序的聚合体。 在此工作中, 我们提议扩展神经型组合的神经形式。 新的合用方程式的构造包括几种向外神经网络, 每个顺序都使用一种。 此外, 我们提议将计算域分割成子域的分解方法。 神经形式在每一个子域中都得到了解决, 而内部网格点相互重叠是为了提供整个碎裂的初始值。 我们在实验中说明, 相交替式的神经形式与高度的精确度和地块的初始质质质质可以解决。