Counterfactual Effect Generalization: A Combinatorial Definition

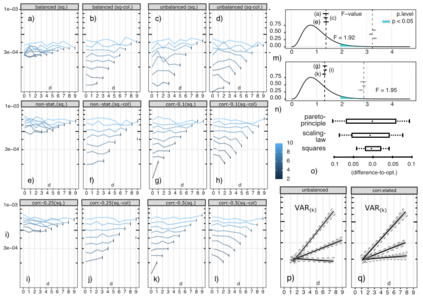
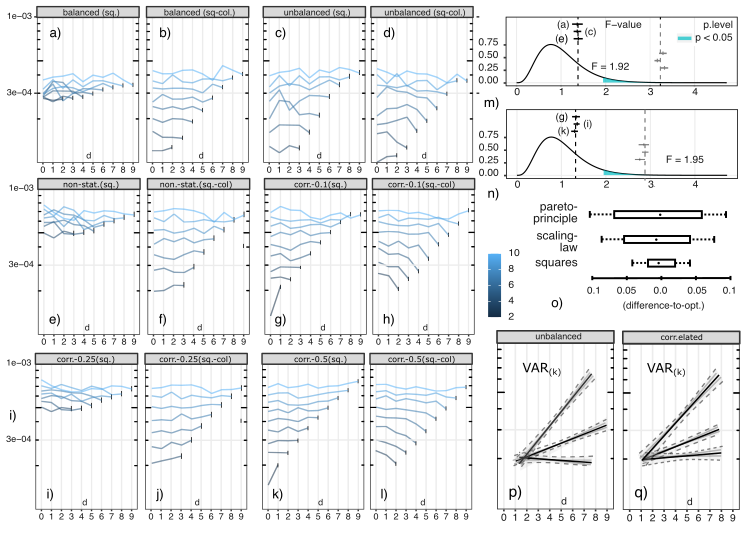
The widely used 'Counterfactual' definition of Causal Effects was derived for unbiasedness and accuracy - and not generalizability. We propose a Combinatorial definition for the External Validity (EV) of intervention effects. We first define the concept of an effect observation 'background'. We then formulate conditions for effect generalization based on their sets of (observable and unobservable) backgrounds. This reveals two limits for effect generalization: (1) when effects are observed under all their enumerable backgrounds, or, (2) when backgrounds have become sufficiently randomized. We use the resulting combinatorial framework to re-examine several issues in the original counterfactual formulation: out-of-sample validity, concurrent estimation of multiple effects, bias-variance tradeoffs, statistical power, and connections to current predictive and explaining techniques. Methodologically, the definitions also allow us to also replace the parametric estimation problems that followed the counterfactual definition by combinatorial enumeration and randomization problems in non-experimental samples. We use this non-parametric framework to demonstrate (External Validity, Unconfoundness and Precision) tradeoffs in the performance of popular supervised, explaining, and causal-effect estimators. We demonstrate the approach also allows for the use of these methods in non-i.i.d. samples. The COVID19 pandemic highlighted the need for learning solutions to provide predictions in severally incomplete samples. We demonstrate applications in this pressing problem.