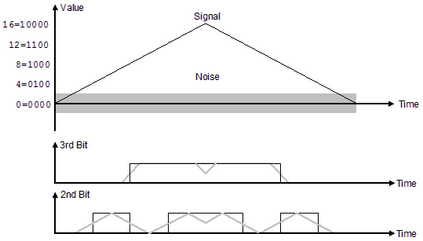
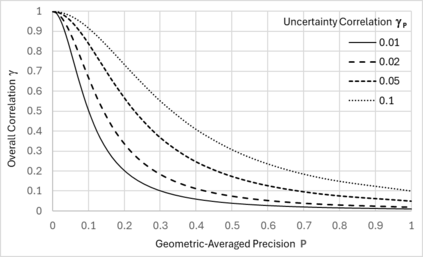
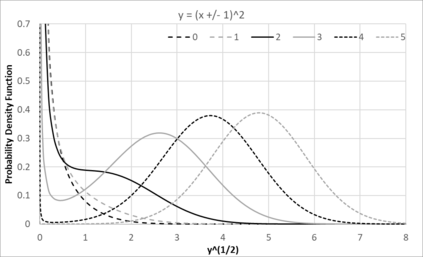
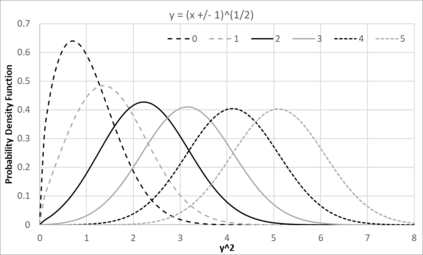
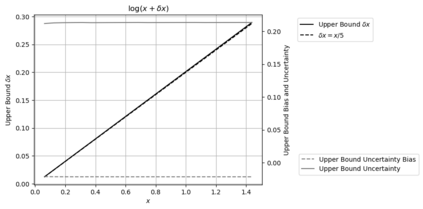
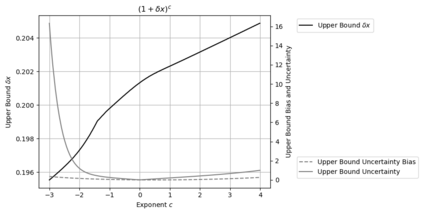
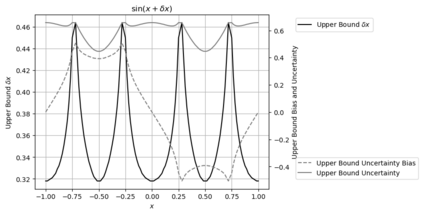
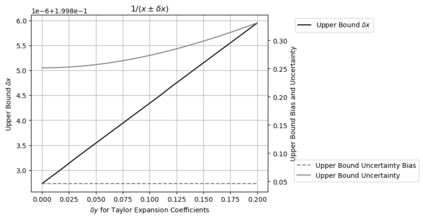
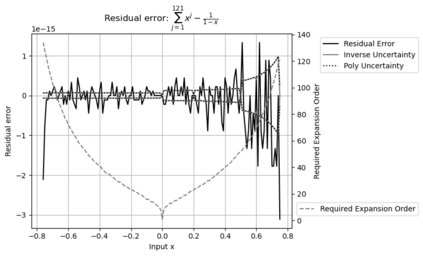
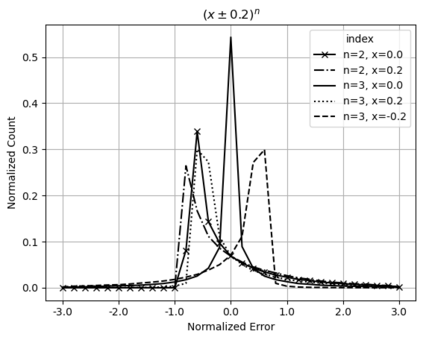
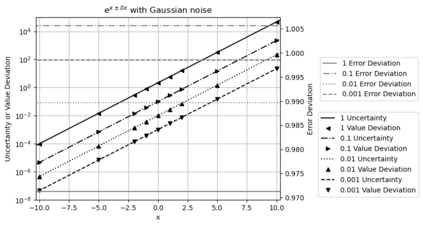
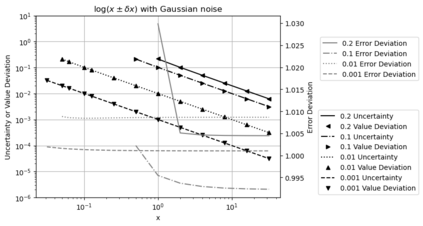
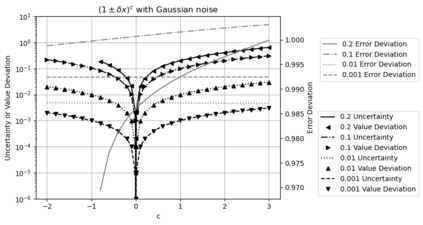
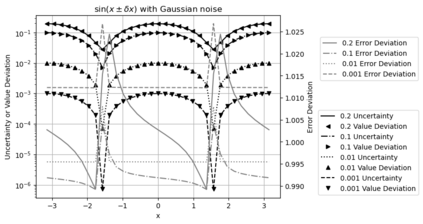
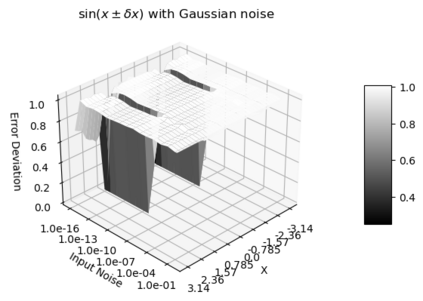
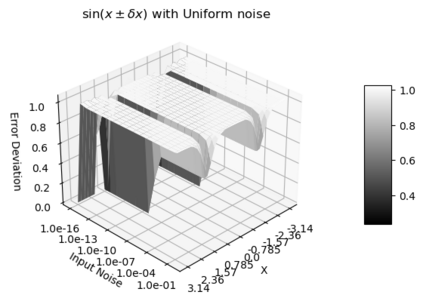
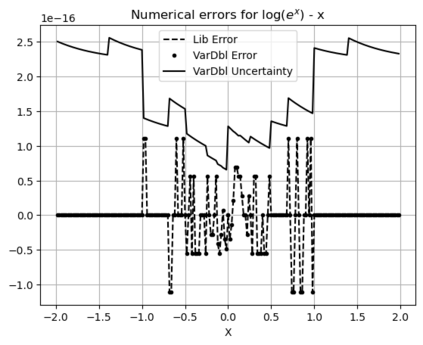
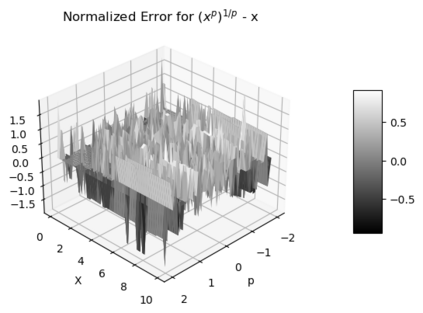
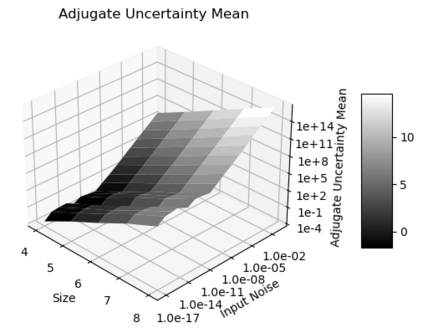
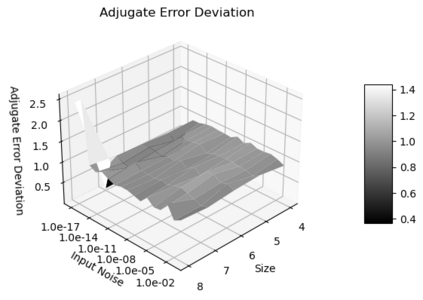
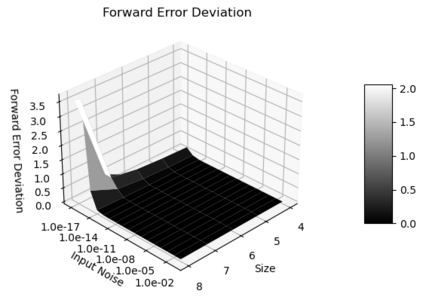
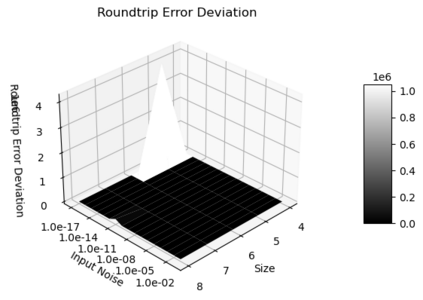
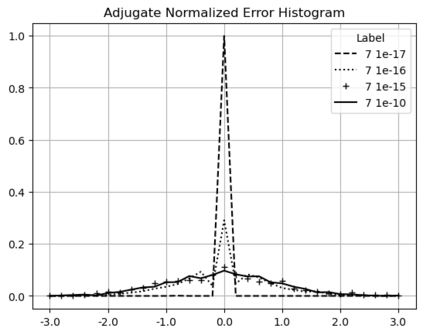
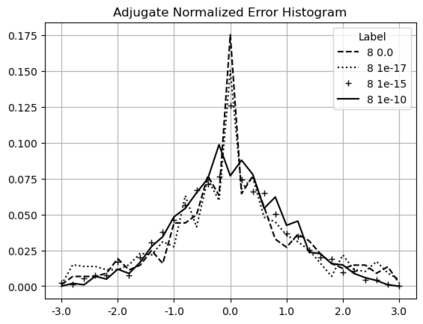
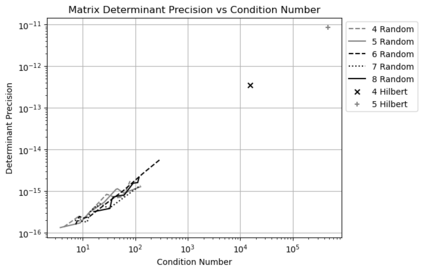
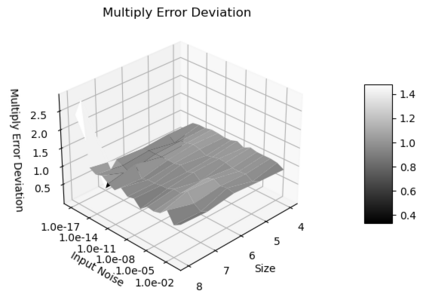
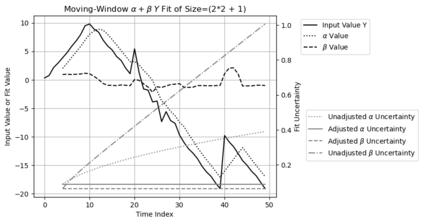
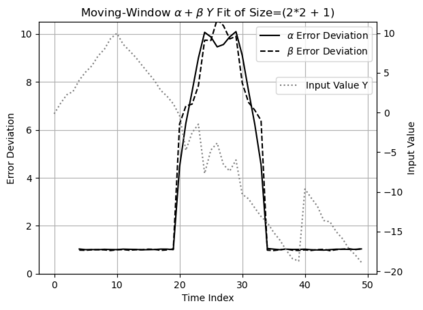
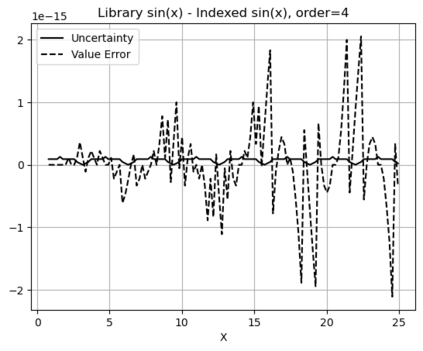
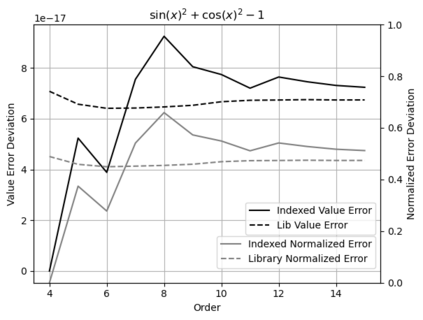
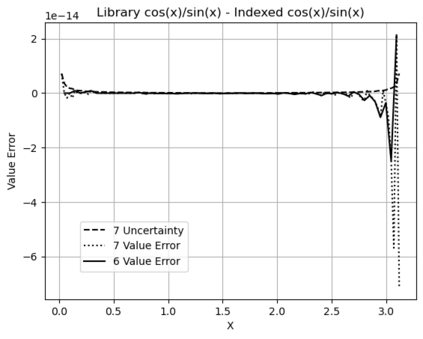
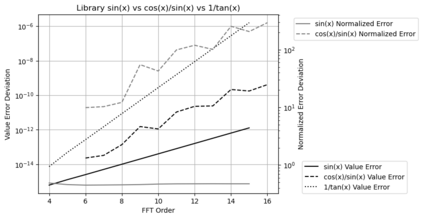
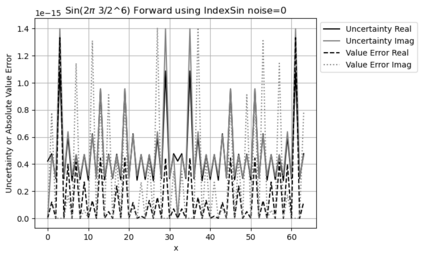
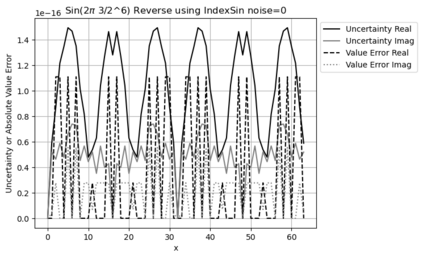
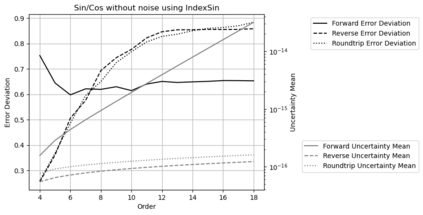
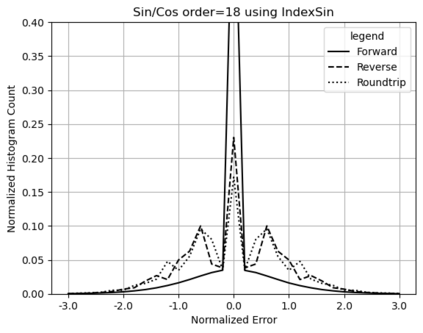
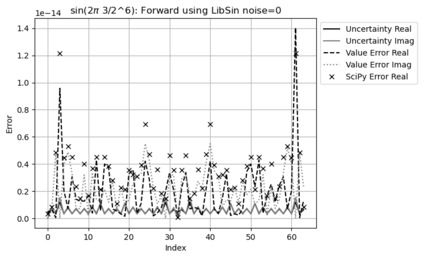
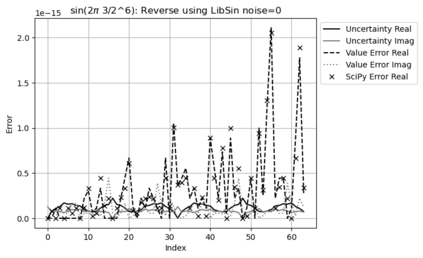
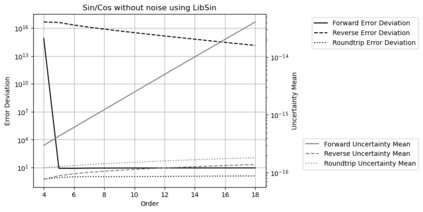
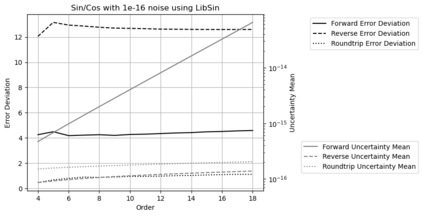
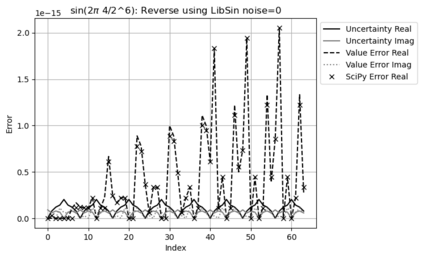
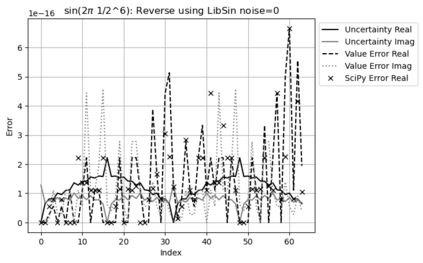
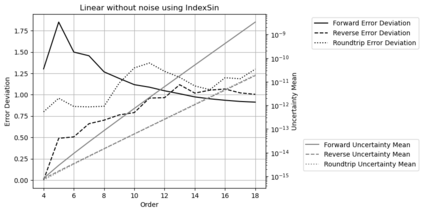
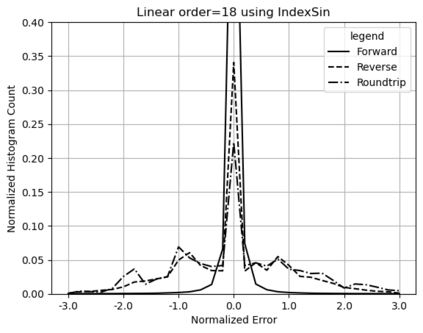
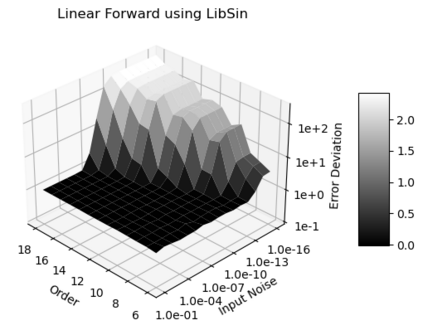
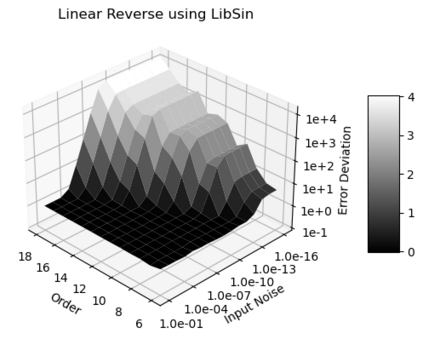
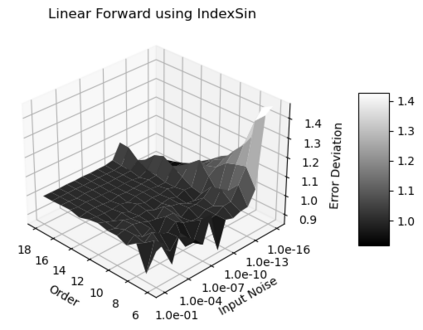
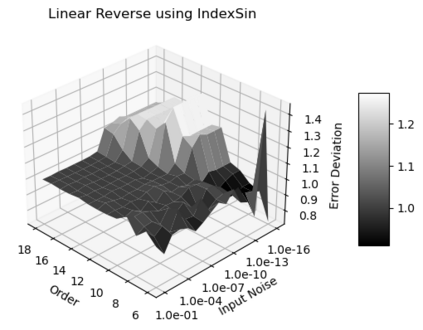
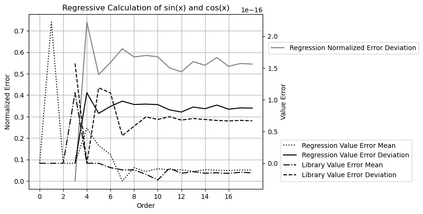
Statistical Taylor Expansion

Statistical Taylor expansion replaces the input precise variables in a conventional Taylor expansion with random variables each with known distribution, to calculate the result mean and deviation. It is based on the uncorrelated uncertainty assumption: Each input variable is measured independently with fine enough statistical precision, so that their uncertainties are independent of each other. Statistical Taylor expansion reviews that the intermediate analytic expressions can no longer be regarded as independent of each other, and the result of analytic expression should be path independent. This conclusion differs fundamentally from the conventional common approach in applied mathematics to find the best execution path for a result. This paper also presents an implementation of statistical Taylor expansion called variance arithmetic, and the tests on variance arithmetic.