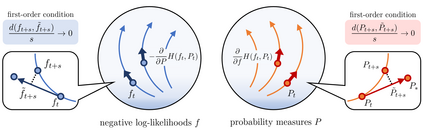
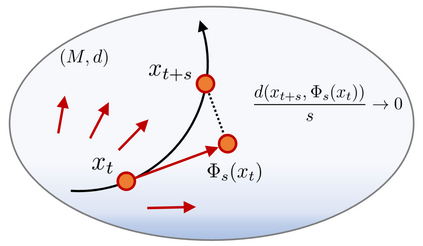
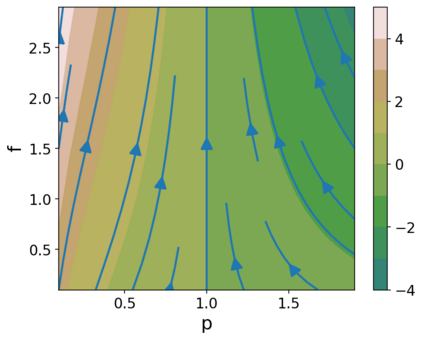
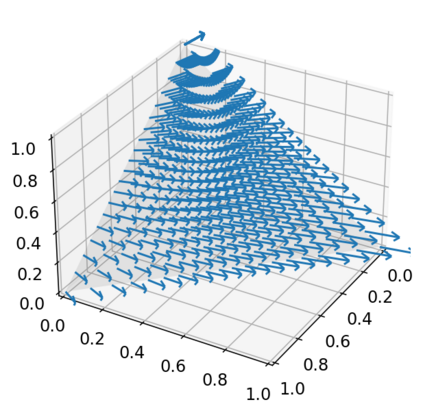
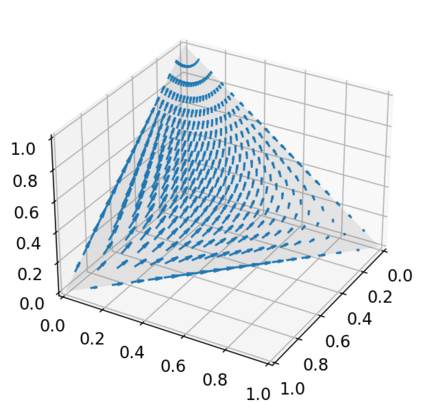
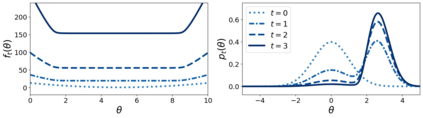
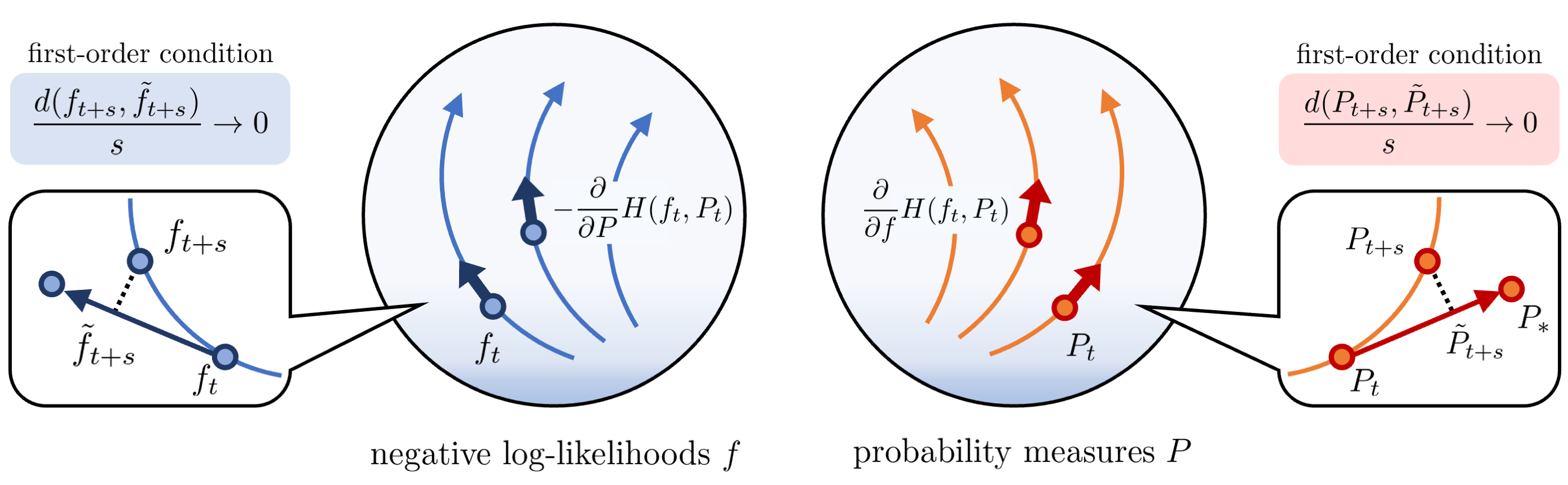
This paper advances theoretical understanding of infinite-dimensional geometrical properties associated with Bayesian inference. First, we introduce a novel class of infinite-dimensional Hamiltonian systems for saddle Hamiltonian functions whose domains are metric spaces. A flow of this system is generated by a Hamiltonian arc field, an analogue of Hamiltonian vector fields formulated based on (i) the first variation of Hamiltonian functions and (ii) the notion of arc fields that extends vector fields to metric spaces. We establish that this system obeys the conservation of energy. We derive a condition for the existence of the flow, which reduces to local Lipschitz continuity of the first variation under sufficient regularity. Second, we present a system of a Hamiltonian function, called the minimum free energy, whose domain is a metric space of negative log-likelihoods and probability measures. The difference of the posterior and the prior of Bayesian inference is characterised as the first variation of the minimum free energy. Our result shows that a transition from the prior to the posterior defines an arc field on a space of probability measures, which forms a Hamiltonian arc field together with another corresponding arc field on a space of negative log-likelihoods. This reveals the underlying invariance of the free energy behind the arc field.
翻译:暂无翻译