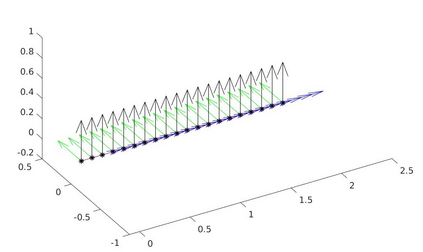
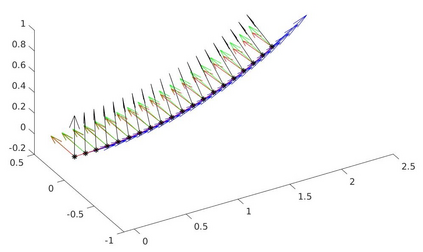
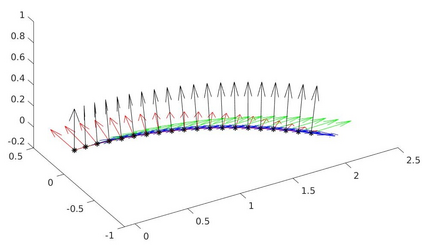
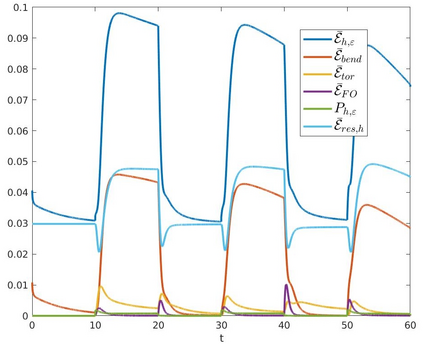
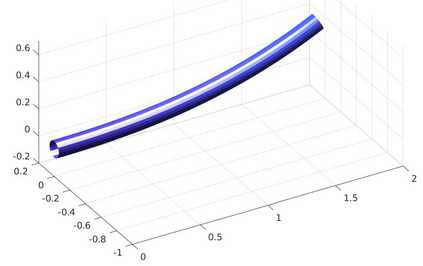
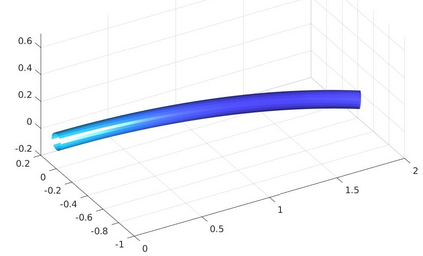
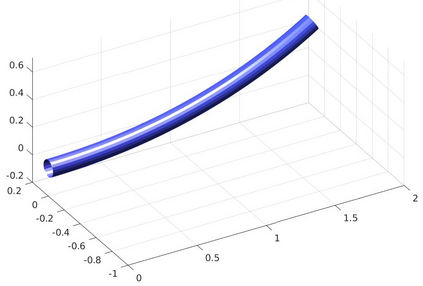
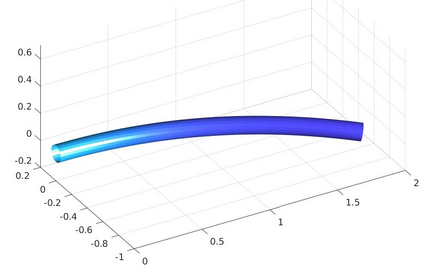
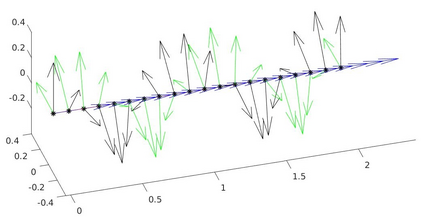
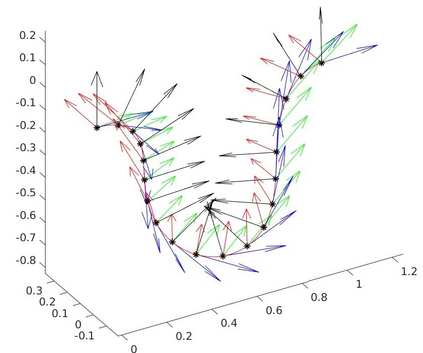
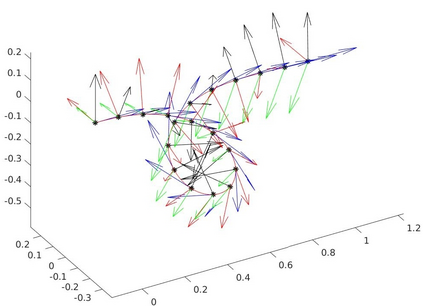
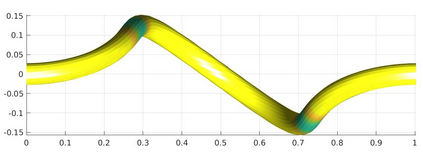
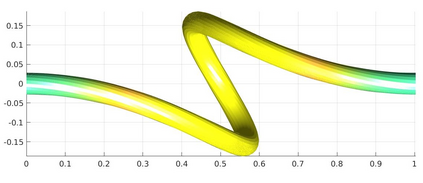
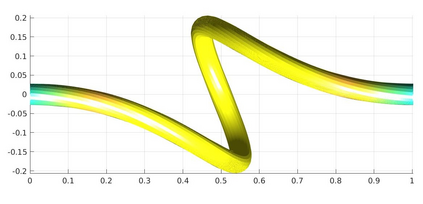
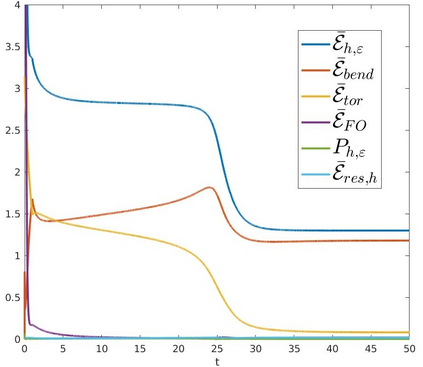
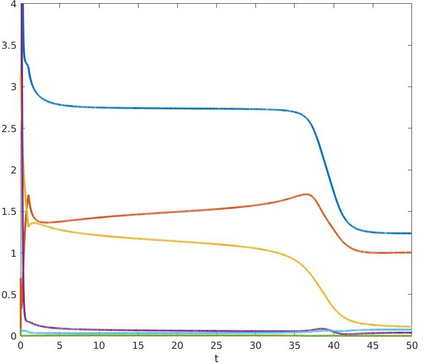
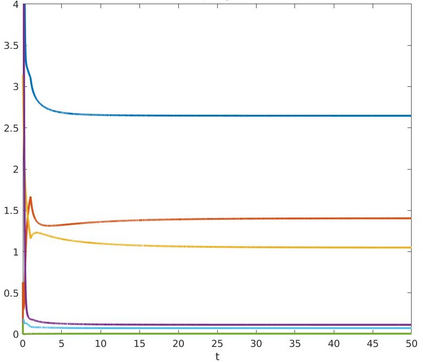
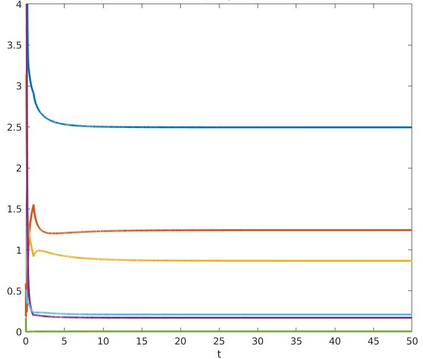
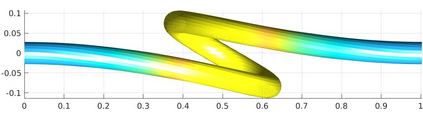
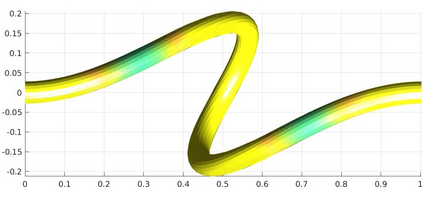
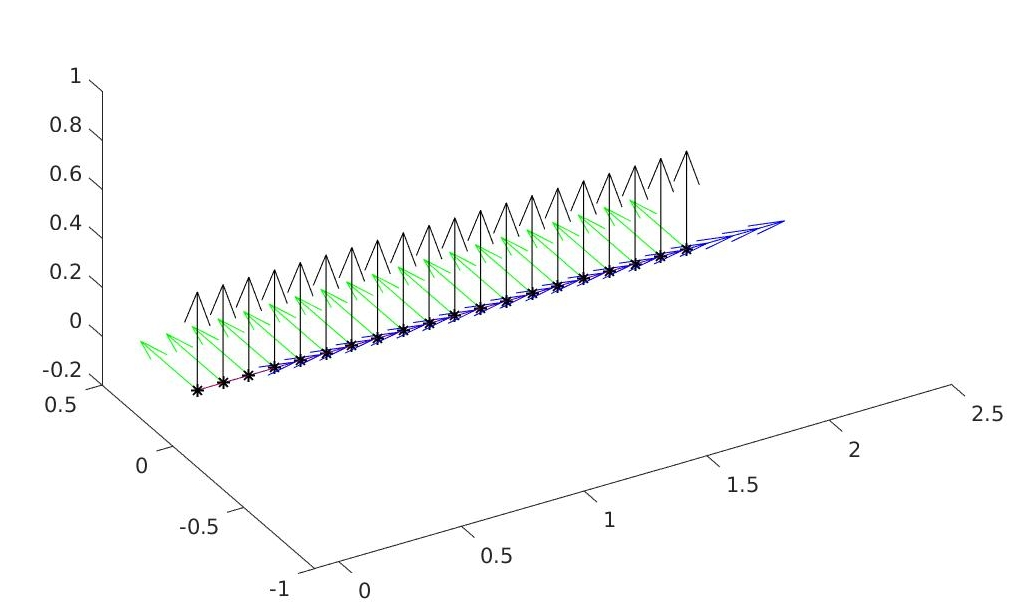
We introduce a nonlinear, one-dimensional bending-twisting model for an inextensible bi-rod that is composed of a nematic liquid crystal elastomer. The model combines an elastic energy that is quadratic in curvature and torsion with a Frank-Oseen energy for the liquid crystal elastomer. Moreover, the model features a nematic-elastic coupling that relates the crystalline orientation with a spontaneous bending-twisting term. We show that the model can be derived as a $\Gamma$-limit from three-dimensional nonlinear elasticity. Moreover, we introduce a numerical scheme to compute critical points of the bending-twisting model via a discrete gradient flow. We present various numerical simulations that illustrate the rich mechanical behavior predicted by the model. The numerical experiments reveal good stability and approximation properties of the method.
翻译:我们引入了一个非线性、一维弯曲-交错模型,用于一个不可扩展的双曲线模型,该模型由一个无线液晶晶体弹性体组成。该模型将一个在曲率和压力中具有二次方位的弹性能源与液晶体弹性体的弗兰克-奥西恩能量结合起来。此外,该模型具有一个与晶体方向和一个自发弯曲-交错术语相联系的线性弹性组合。我们显示,该模型可以从三维非线性非线性弹性性中得出一个$\Gamma$的极限。此外,我们引入了一个数字方案,通过离散梯度流来计算弯曲-线性模型的临界点。我们提出了各种数字模拟,以说明模型所预测的丰富的机械行为。数字实验揭示了该方法的良好稳定性和近似特性。