Power-divergence copulas: A new class of Archimedean copulas, with an insurance application

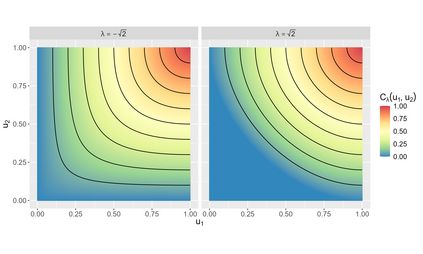
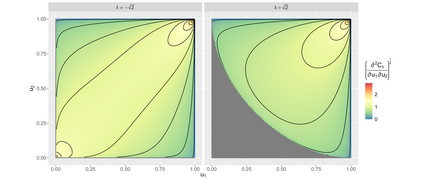
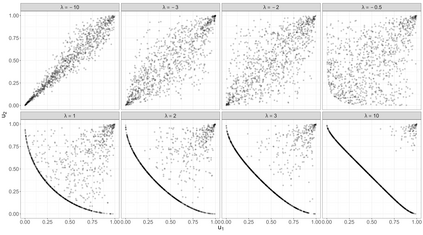
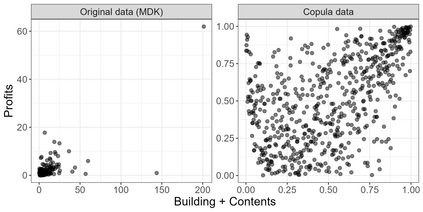
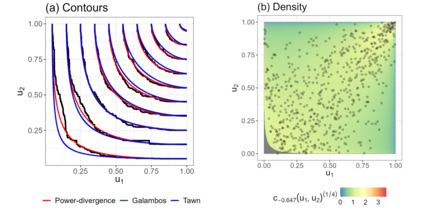
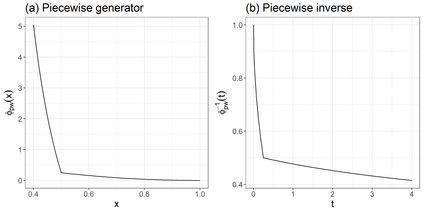
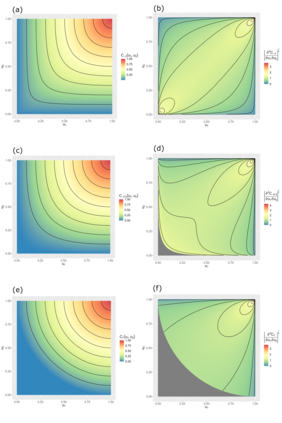
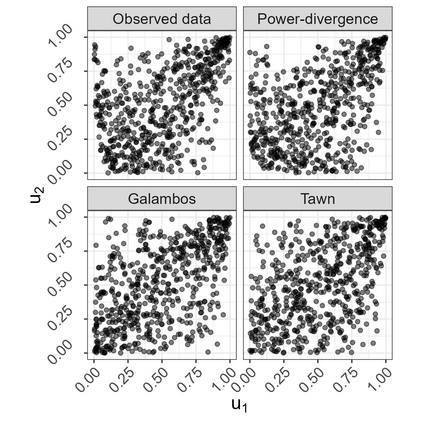
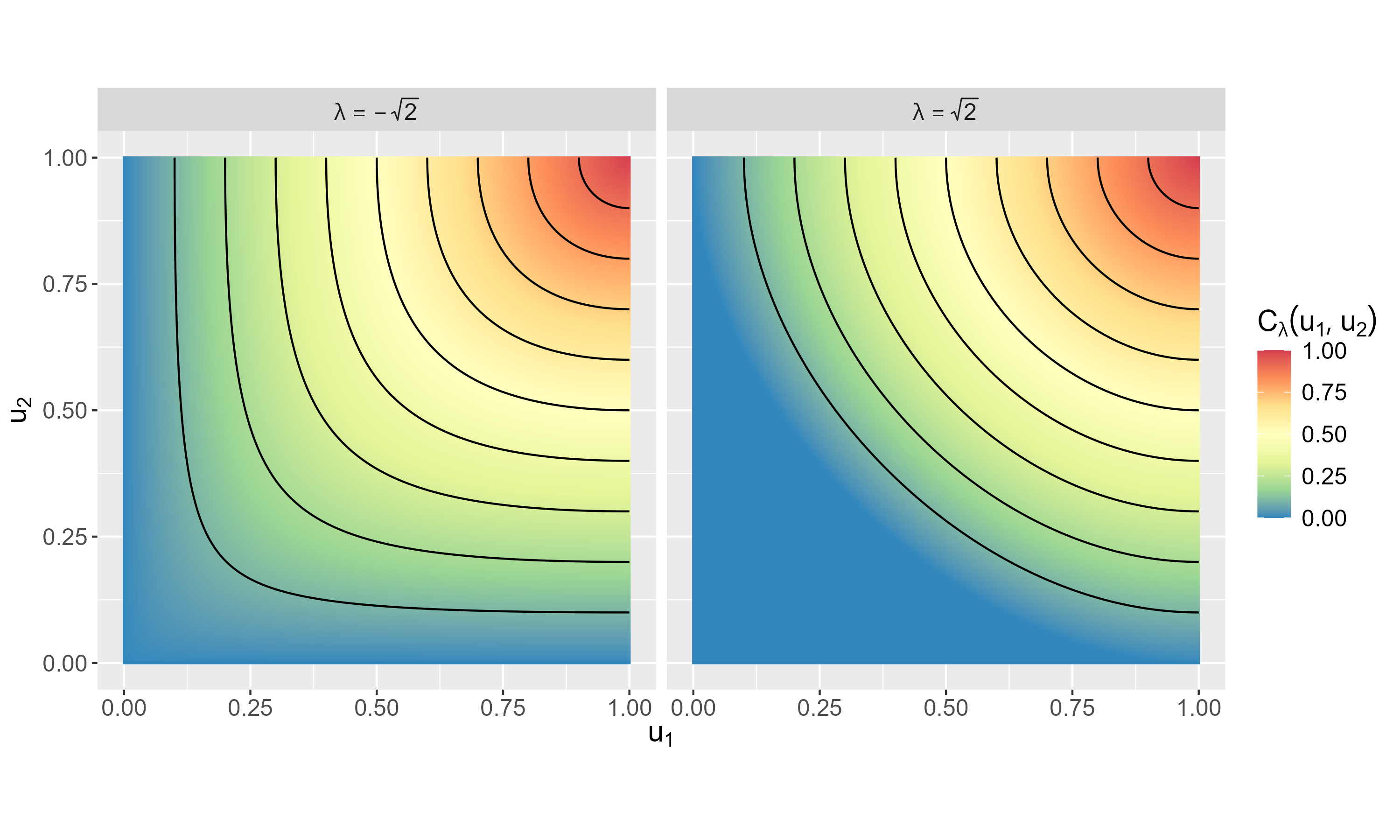
This paper demonstrates that, under a particular convention, the convex functions that characterise the phi divergences also generate Archimedean copulas in at least two dimensions. As a special case, we develop the family of Archimedean copulas associated with the important family of power divergences, which we call the power-divergence copulas. The properties of the family are extensively studied, including the subfamilies that are absolutely continuous or have a singular component, the ordering of the family, limiting cases (i.e., the Frechet-Hoeffding lower bound and Frechet-Hoeffding upper bound), the Kendall's tau and tail-dependence coefficients, and cases that extend to three or more dimensions. In an illustrative application, the power-divergence copulas are used to model a Danish fire insurance dataset. It is shown that the power-divergence copulas provide an adequate fit to the bivariate distribution of two kinds of fire-related losses claimed by businesses, while several benchmarks (a suite of well known Archimedean, extreme-value, and elliptical copulas) do not.