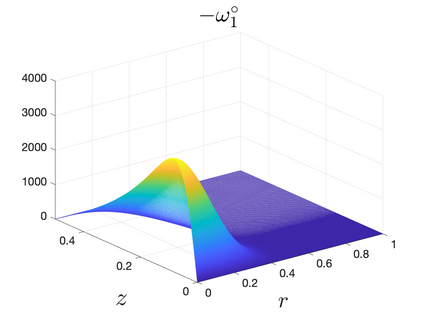
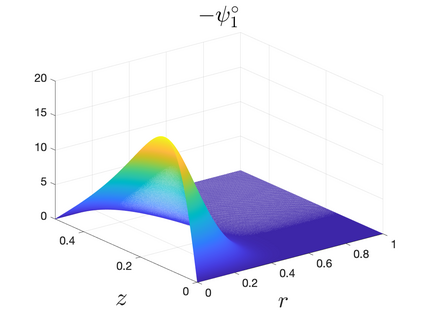
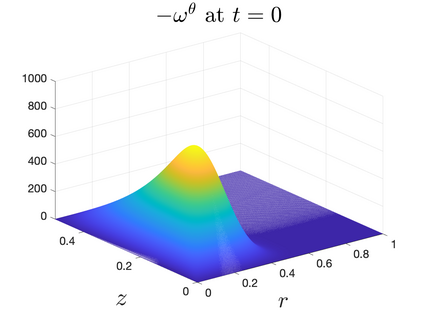
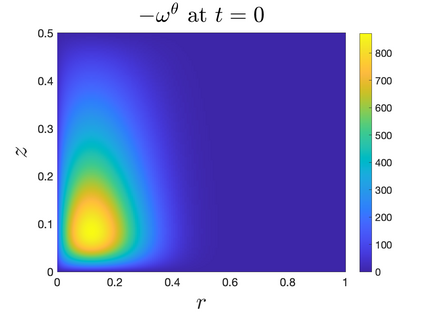
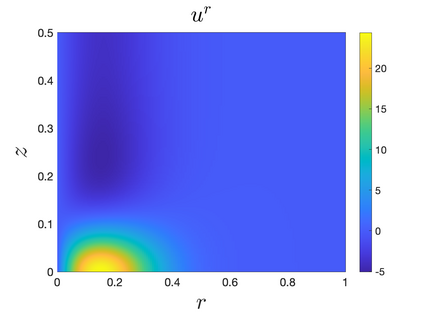
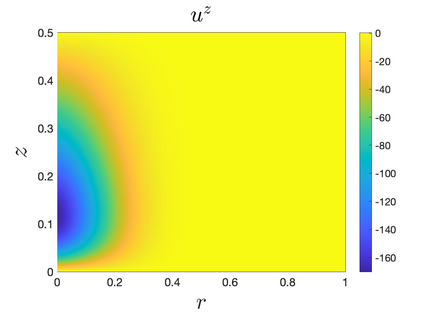
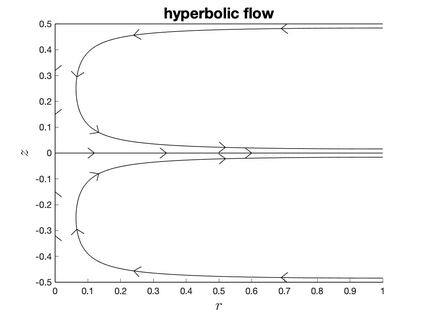
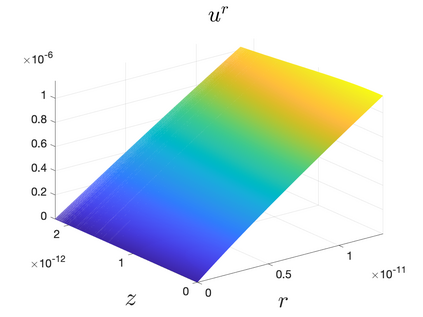
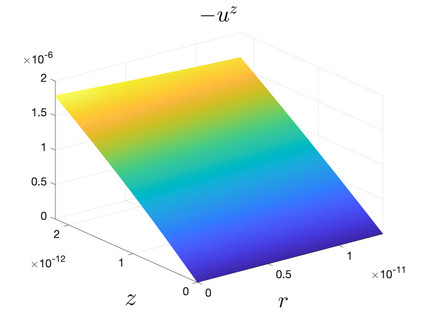
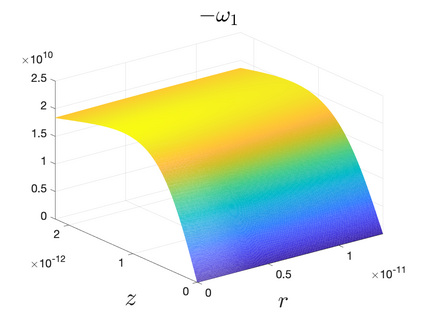
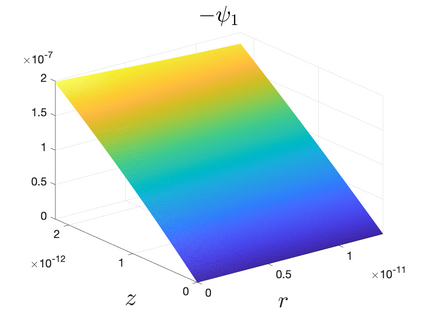
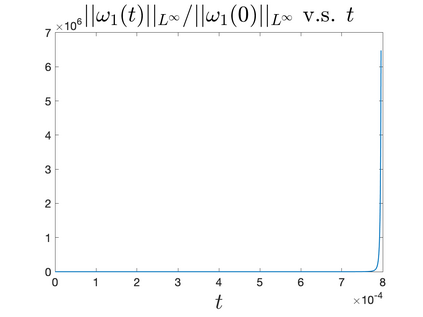
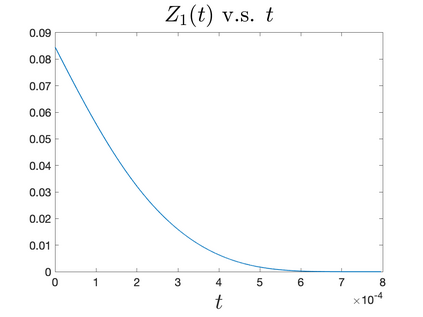
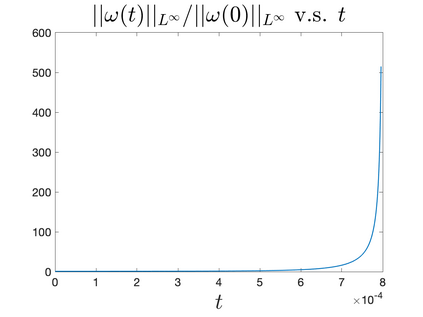
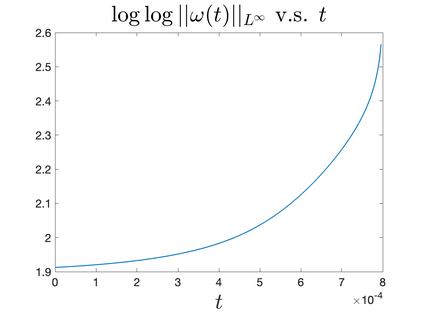
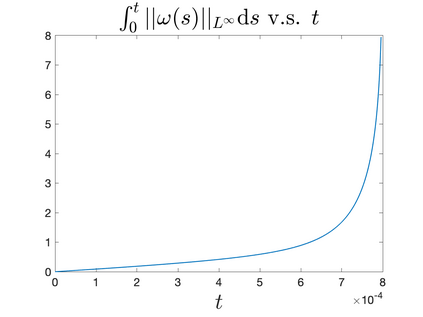
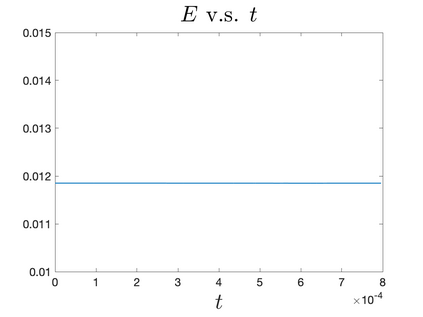
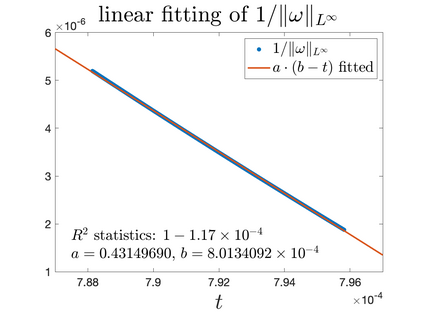
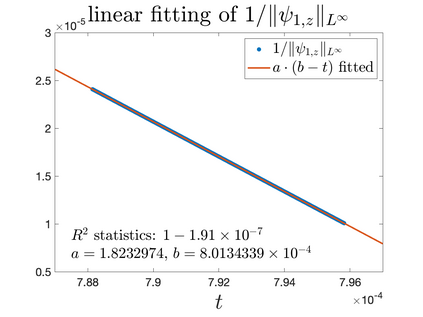
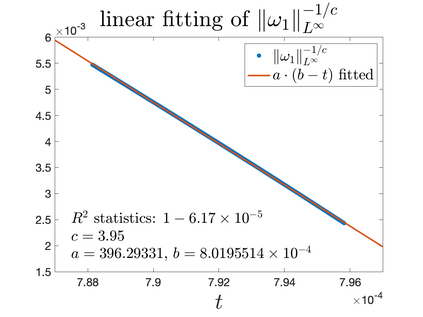
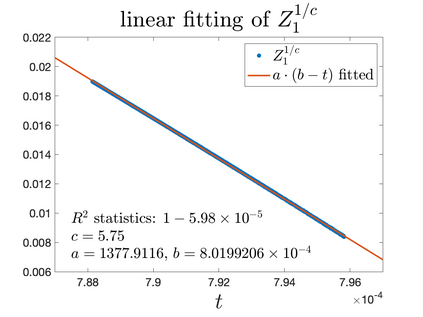
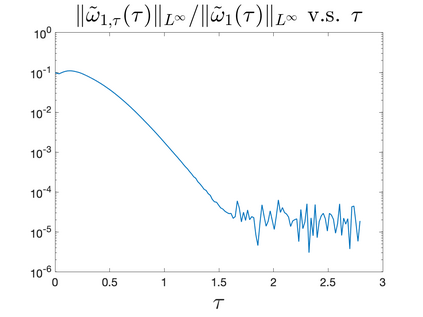
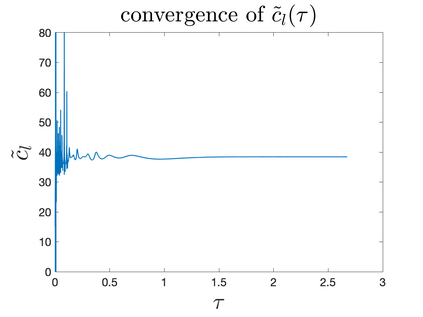
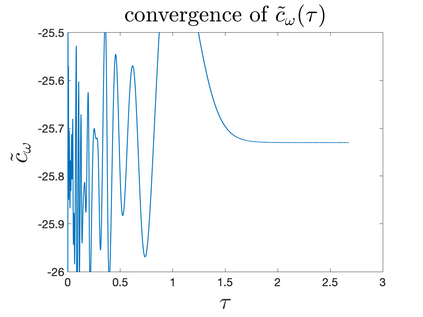
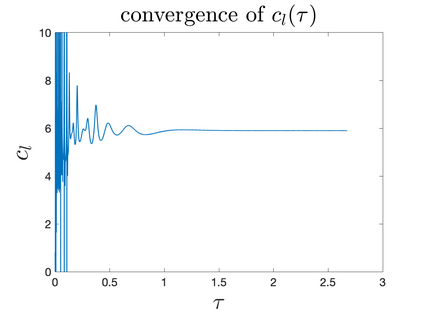
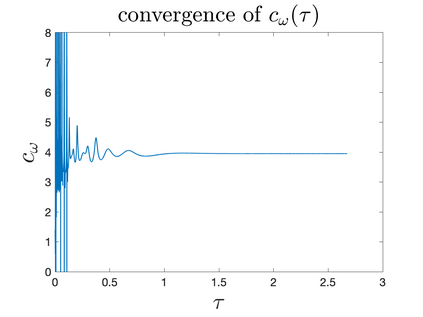
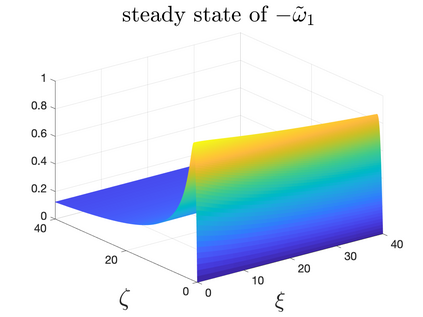
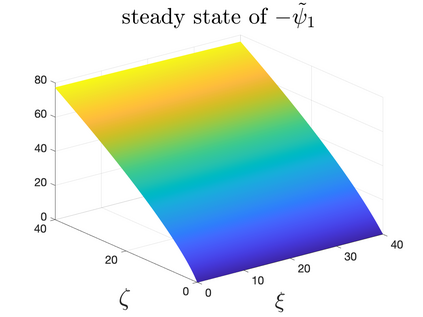
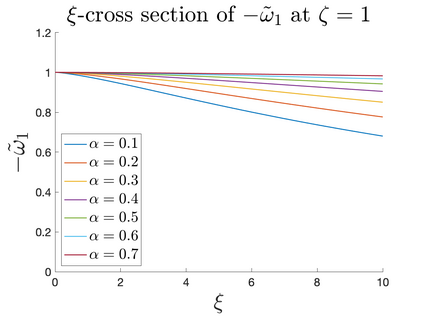
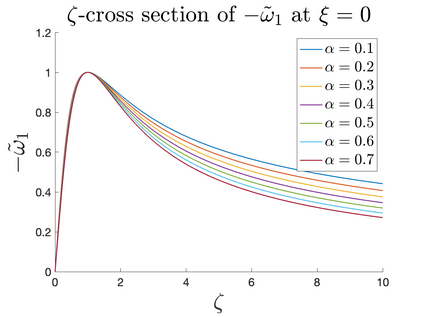
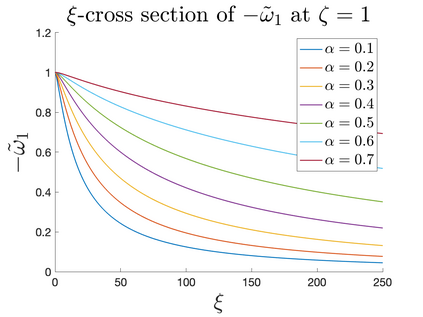
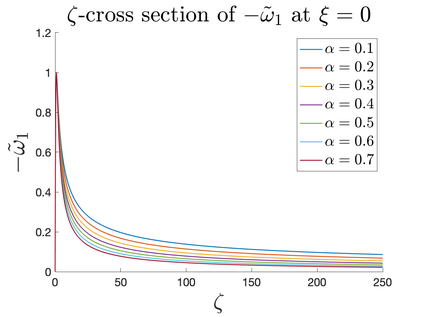
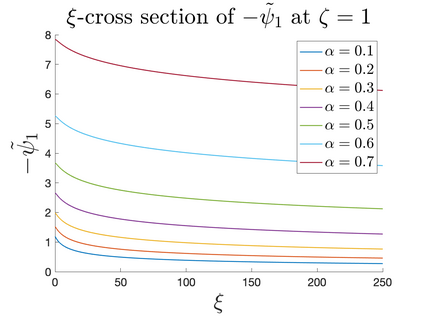
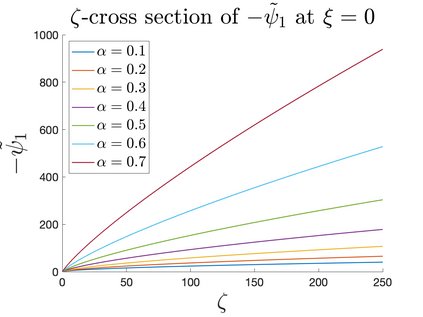
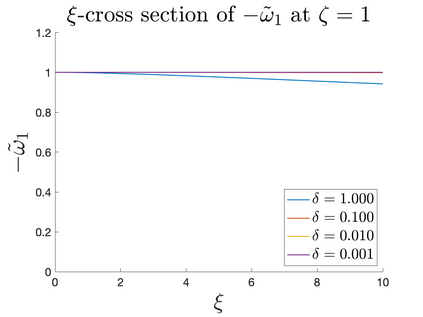
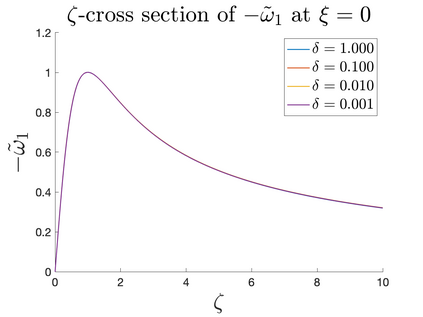
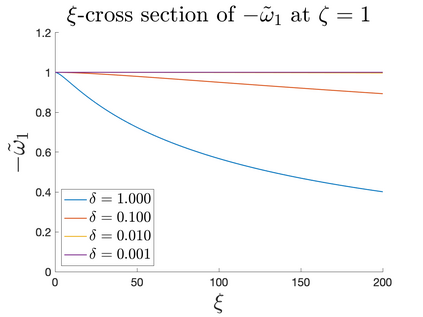
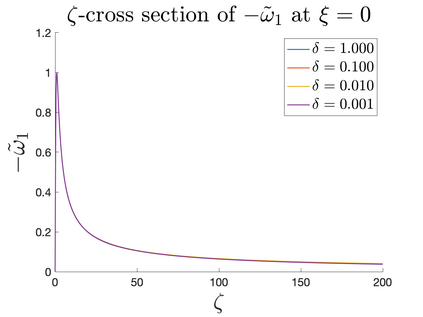
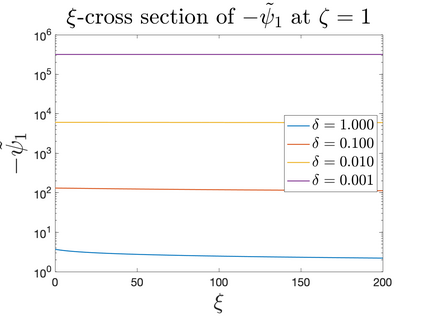
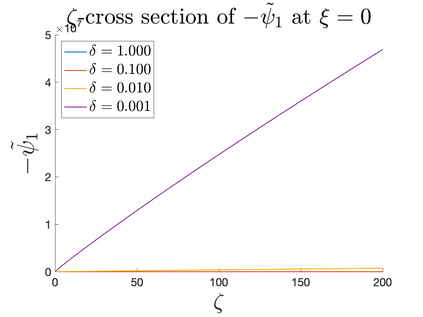
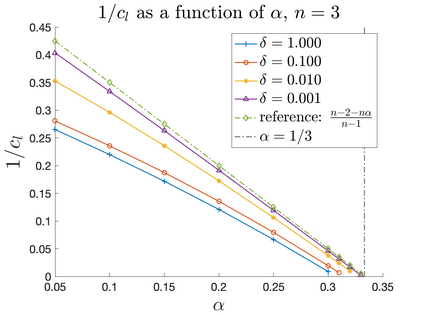
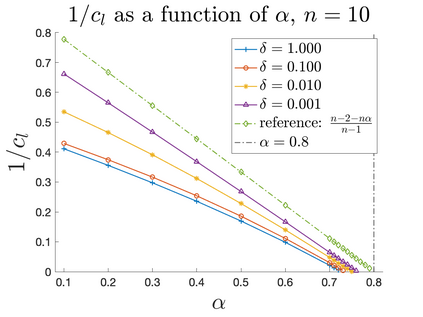
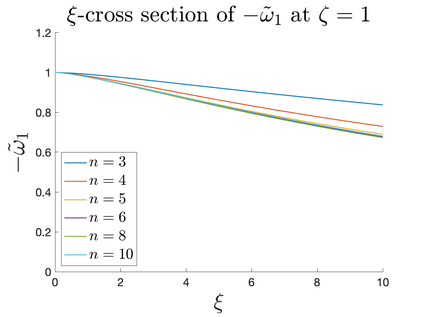
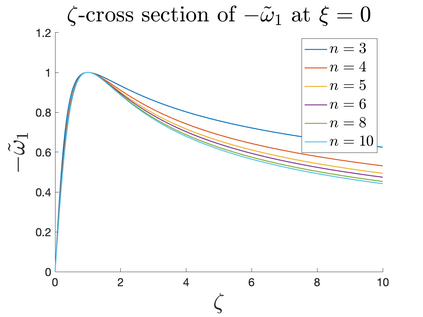
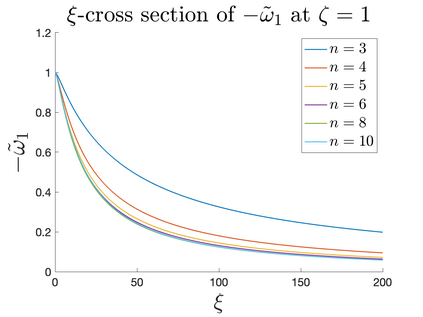
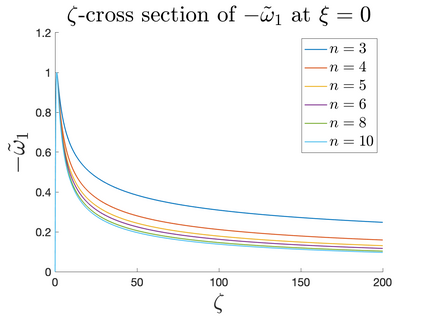
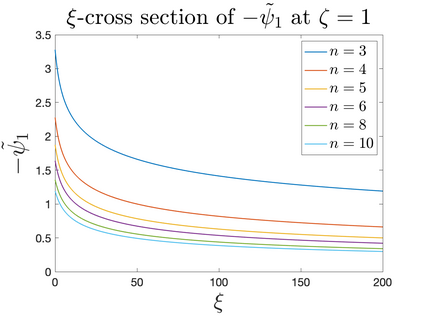
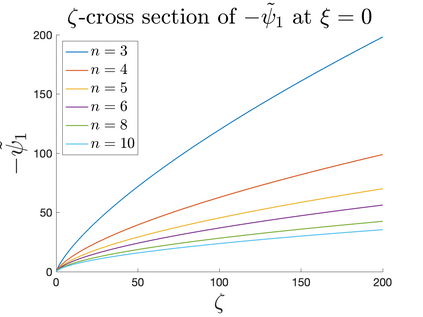
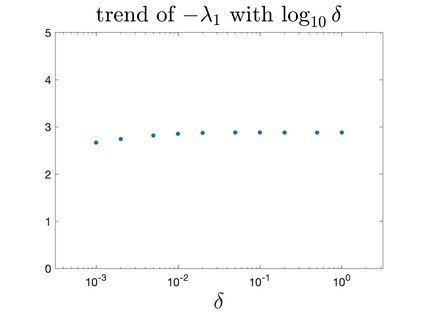
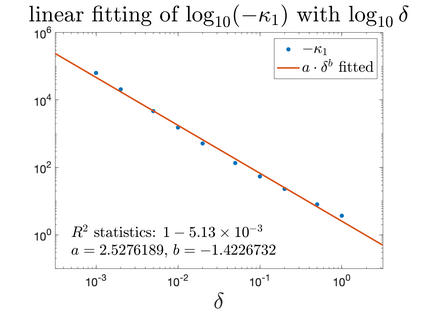
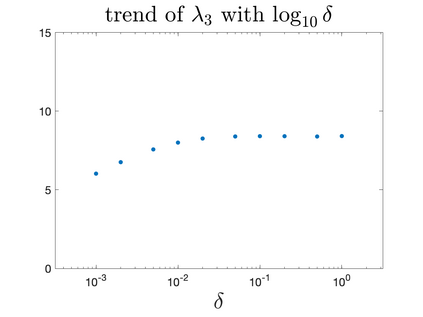
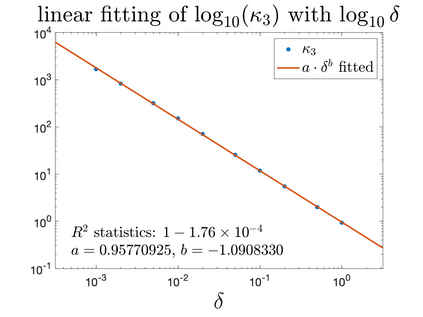
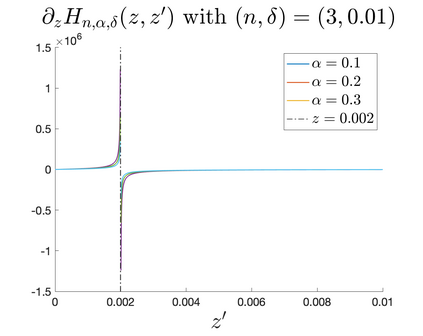
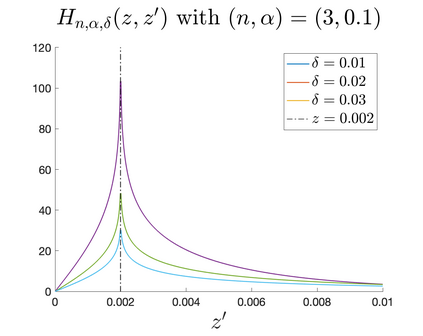
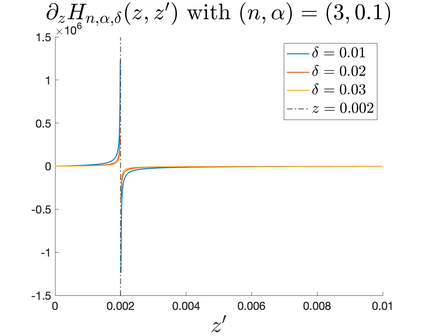
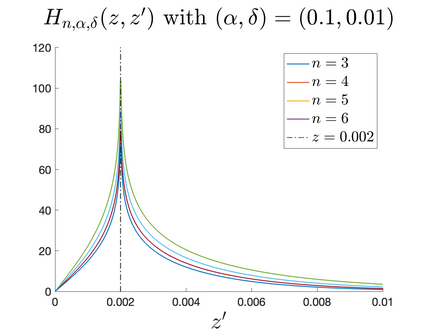
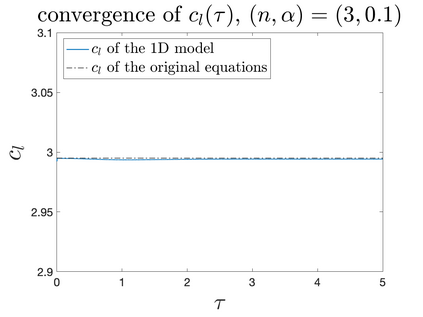
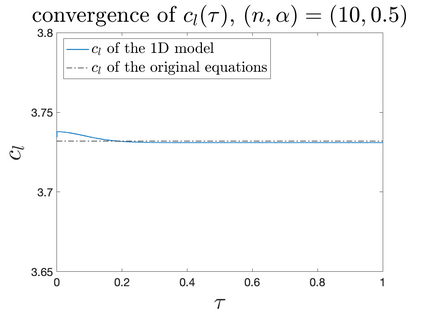
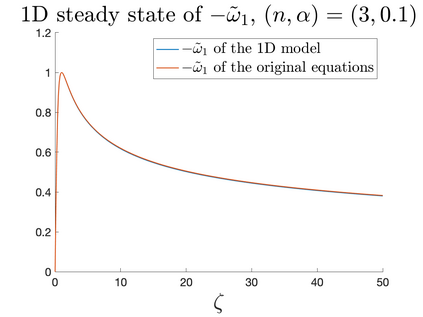
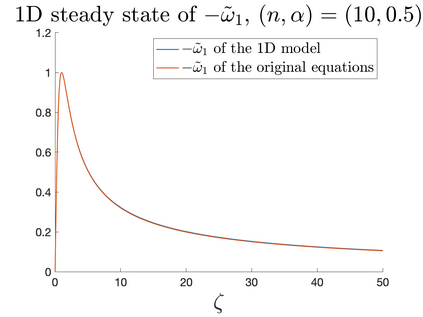
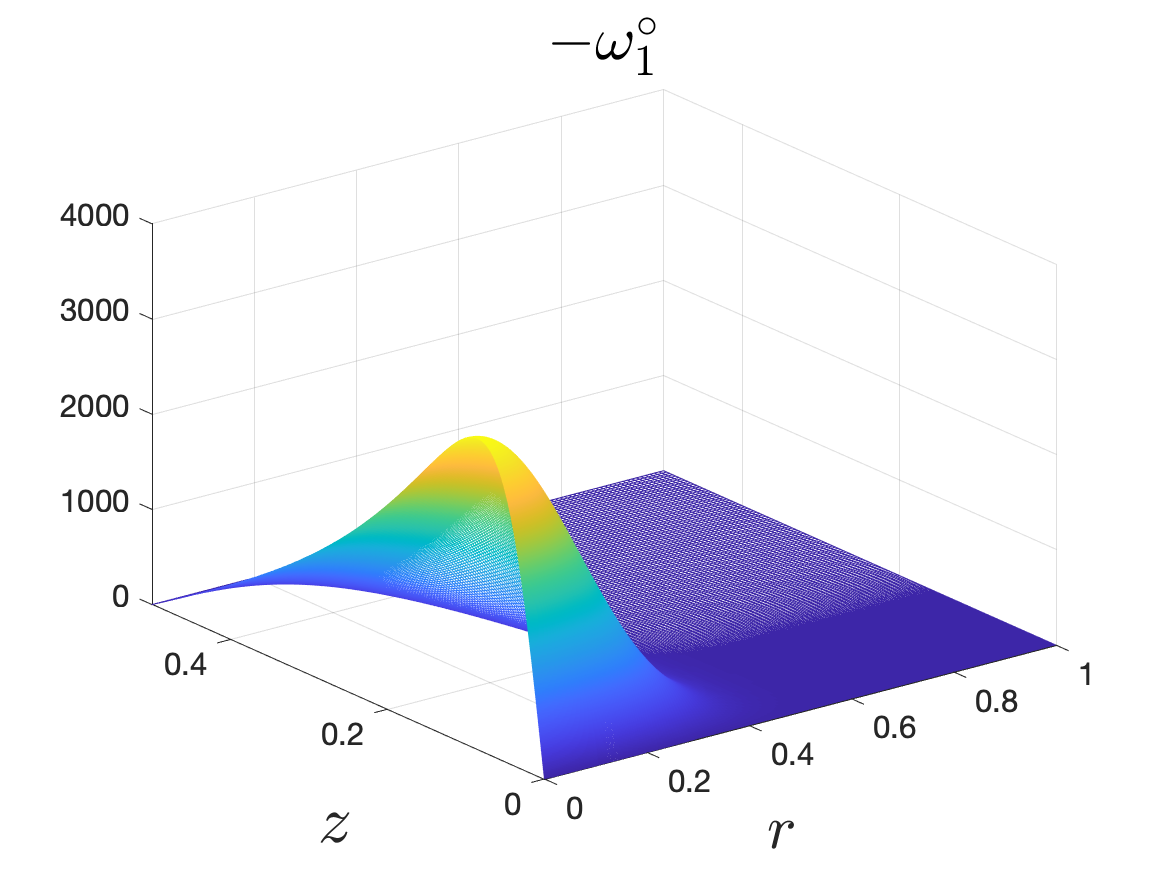
In Part II of this sequence to our previous paper for the 3-dimensional Euler equations \cite{zhang2022potential}, we investigate potential singularity of the $n$-diemnsional axisymmetric Euler equations with $C^\alpha$ initial vorticity for a large range of $\alpha$. We use the adaptive mesh method to solve the $n$-dimensional axisymmetric Euler equations and use the scaling analysis and dynamic rescaling method to examine the potential blow-up and capture its self-similar profile. Our study shows that the $n$-dimensional axisymmetric Euler equations with our initial data develop finite-time blow-up when the H\"{o}lder exponent $\alpha<\alpha^*$, and this upper bound $\alpha^*$ can asymptotically approach $1-\frac{2}{n}$. Moreover, we introduce a stretching parameter $\delta$ along the $z$-direction. Based on a few assumptions inspired by our numerical experiments, we obtain $\alpha^*=1-\frac{2}{n}$ by studying the limiting case of $\delta \rightarrow 0$. For the general case, we propose a relatively simple one-dimensional model and numerically verify its approximation to the $n$-dimensional Euler equations. This one-dimensional model sheds useful light to our understanding of the blowup mechanism for the $n$-dimensional Euler equations. As shown in \cite{zhang2022potential}, the scaling behavior and regularity properties of our initial data are quite different from those of the initial data considered by Elgindi in \cite{elgindi2021finite}.
翻译:我们用适应网格方法来解决 $-dismexial liversial complications {cite{zhang2022prext}} 3维维度方程 {cite{zhang2022lible}} 的上一张纸,我们用此程序来研究美元- liter liter liversion licommer literal compales 的奇特性。我们使用适应网格方法来解决 $n- dismexial literial literial literliteral literality {ctime $_cite diterminality $_cite ditermal litermality $\ lidometitermal litermal_qual dislations listalal legalal legal legal legal_Broup a proup legnal dal deal deal dal dal dal a exal exal a exmal a exal legal deal deal a le le le exmlal exal a le ex exal a exm ex ex ex legal a ex ex legal a ex ex exm ex exmal a exmal lemental a ex exmal lemental a lemental a ex ex ex ex lemental ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex exal a ex ex ex ex ex exal a ex exal exal a ex ex exal a exal a ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex ex