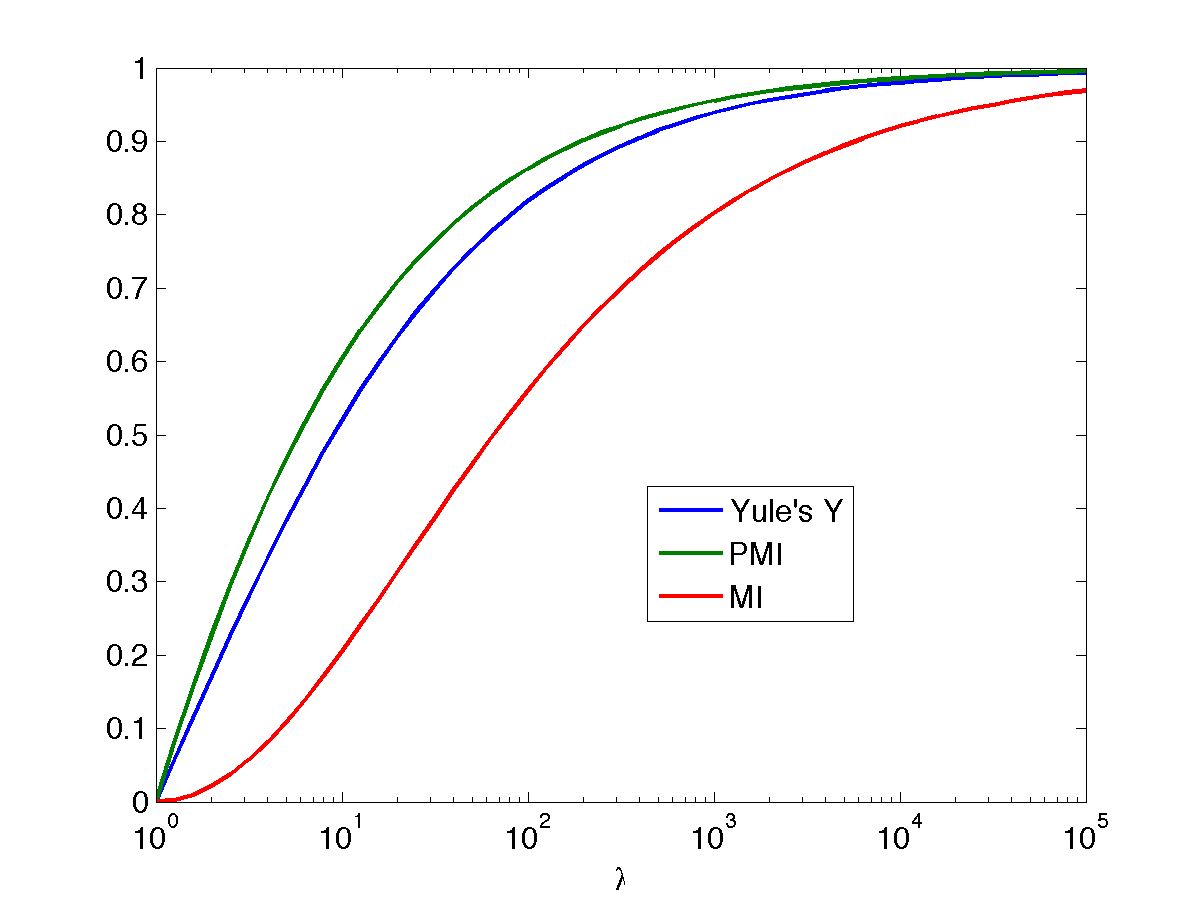
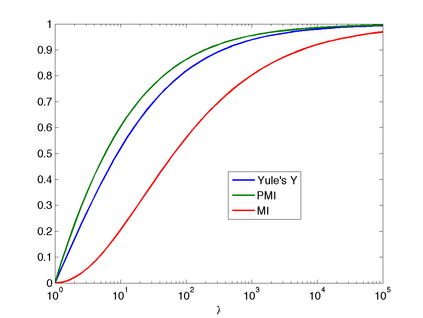
Barlow (1985) hypothesized that the co-occurrence of two events $A$ and $B$ is "suspicious" if $P(A,B) \gg P(A) P(B)$. We first review classical measures of association for $2 \times 2$ contingency tables, including Yule's $Y$ (Yule, 1912), which depends only on the odds ratio $\lambda$, and is independent of the marginal probabilities of the table. We then discuss the mutual information (MI) and pointwise mutual information (PMI), which depend on the ratio $P(A,B)/P(A)P(B)$, as measures of association. We show that, once the effect of the marginals is removed, MI and PMI behave similarly to $Y$ as functions of $\lambda$. The pointwise mutual information is used extensively in some research communities for flagging suspicious coincidences, but it is important to bear in mind the sensitivity of the PMI to the marginals, with increased scores for sparser events.
翻译:巴洛(1985年)假设,如果美元P(A,B)\gg P(A)\(B)\美元P(B),两起事件的共同发生是“可疑”的。我们首先审查传统的关联度2倍于2美元的应急表,包括Yule的Y$(Yule,1912年),这仅取决于几率比率$\lambda$(Ule,1912年),并且独立于该表的边缘概率。然后我们讨论相互信息(MI)和点对点的相互信息(PMI),这取决于美元P(A,B)/P(P)P(B)的比例,作为联系措施。我们表明,一旦边缘效应消除,MI和PMI的功能接近于$Y,相当于$@lambda$(Y)的功能。一些研究社区广泛使用了点对等信息来标出可疑的巧合,但重要的是要牢记PMI对边缘的敏感度,而稀疏漏事件的分数增加。