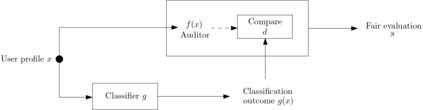
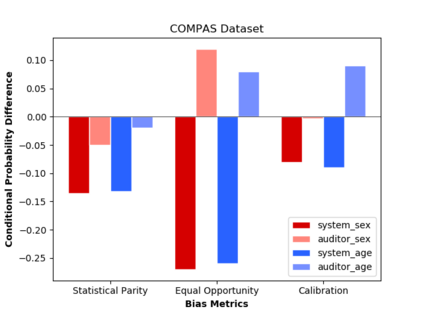
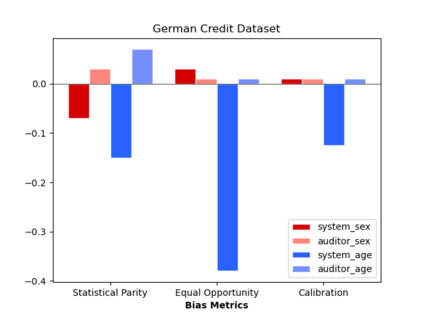
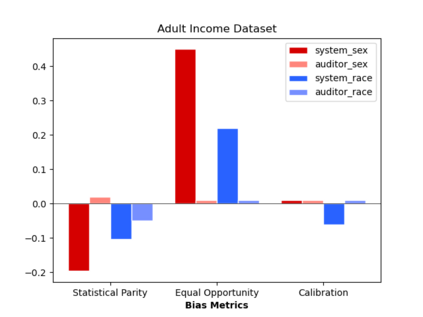
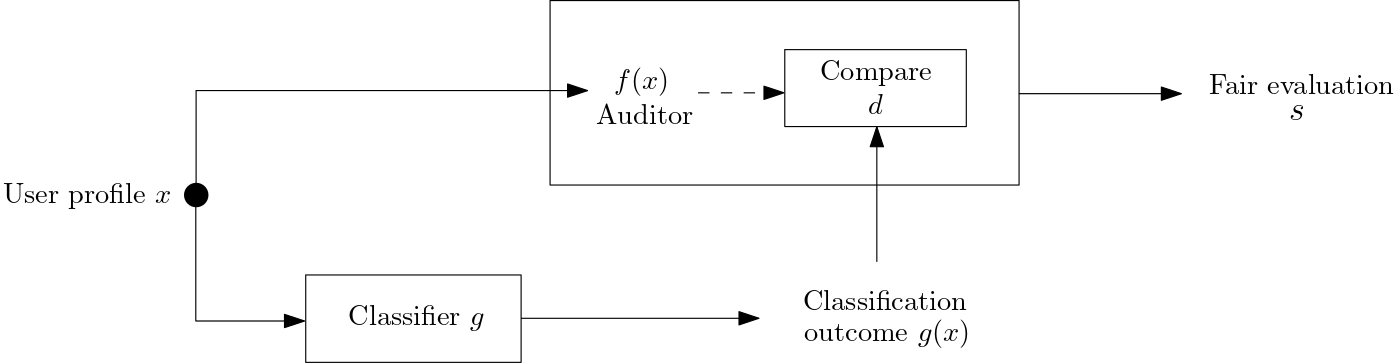
Algorithmic fairness literature presents numerous mathematical notions and metrics, and also points to a tradeoff between them while satisficing some or all of them simultaneously. Furthermore, the contextual nature of fairness notions makes it difficult to automate bias evaluation in diverse algorithmic systems. Therefore, in this paper, we propose a novel model called latent assessment model (LAM) to characterize binary feedback provided by human auditors, by assuming that the auditor compares the classifier's output to his or her own intrinsic judgment for each input. We prove that individual and group fairness notions are guaranteed as long as the auditor's intrinsic judgments inherently satisfy the fairness notion at hand, and are relatively similar to the classifier's evaluations. We also demonstrate this relationship between LAM and traditional fairness notions on three well-known datasets, namely COMPAS, German credit and Adult Census Income datasets. Furthermore, we also derive the minimum number of feedback samples needed to obtain PAC learning guarantees to estimate LAM for black-box classifiers. These guarantees are also validated via training standard machine learning algorithms on real binary feedback elicited from 400 human auditors regarding COMPAS.
翻译:分析公平性文献提出了许多数学概念和衡量标准,也指出了两者之间的权衡,同时对一些或所有概念加以讽刺。此外,公平概念的背景性质使得不同算法系统中的偏向评价难以自动化。因此,我们在本文件中提出了一个称为潜在评估模型的新模式,用以描述人类审计员提供的二元反馈,假设审计员将分类者的输出与对每种输入的自身判断进行比较。我们证明,只要审计员的内在判断本身就符合公平概念,而且与分类者的评价相对相似,个人和群体公平概念就得到保障。我们还展示了LAM与三个众所周知的数据集(即COMPAS、德国信用和成人普查收入数据集)的传统公平概念之间的关系。此外,我们还得出了获得PAC学习保证对黑箱分类员进行LAM估算所需的最低反馈样本数量。这些保证还通过培训机器学习标准算法来验证,该算出从400名人类审计员那里获得的COMPAS的真正二元反馈。