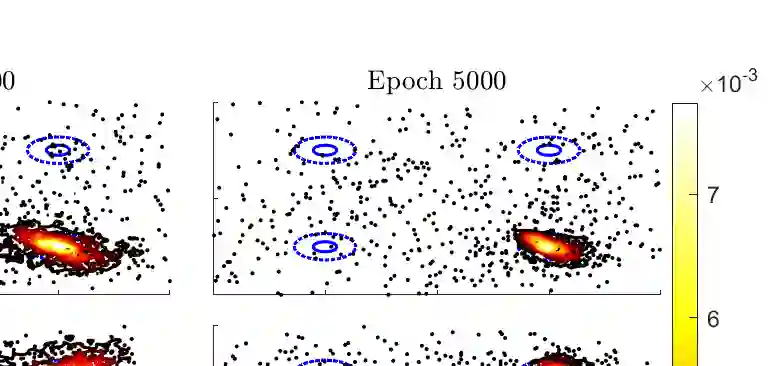
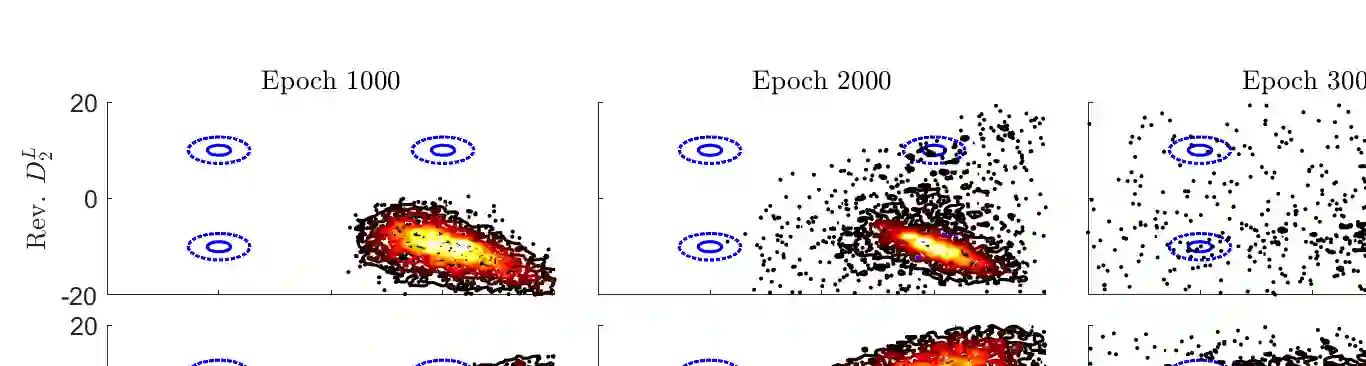
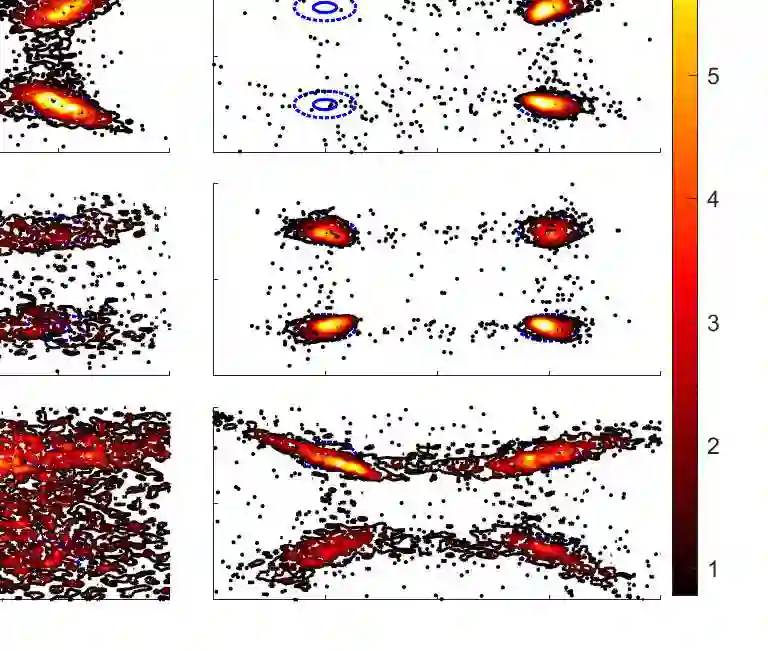
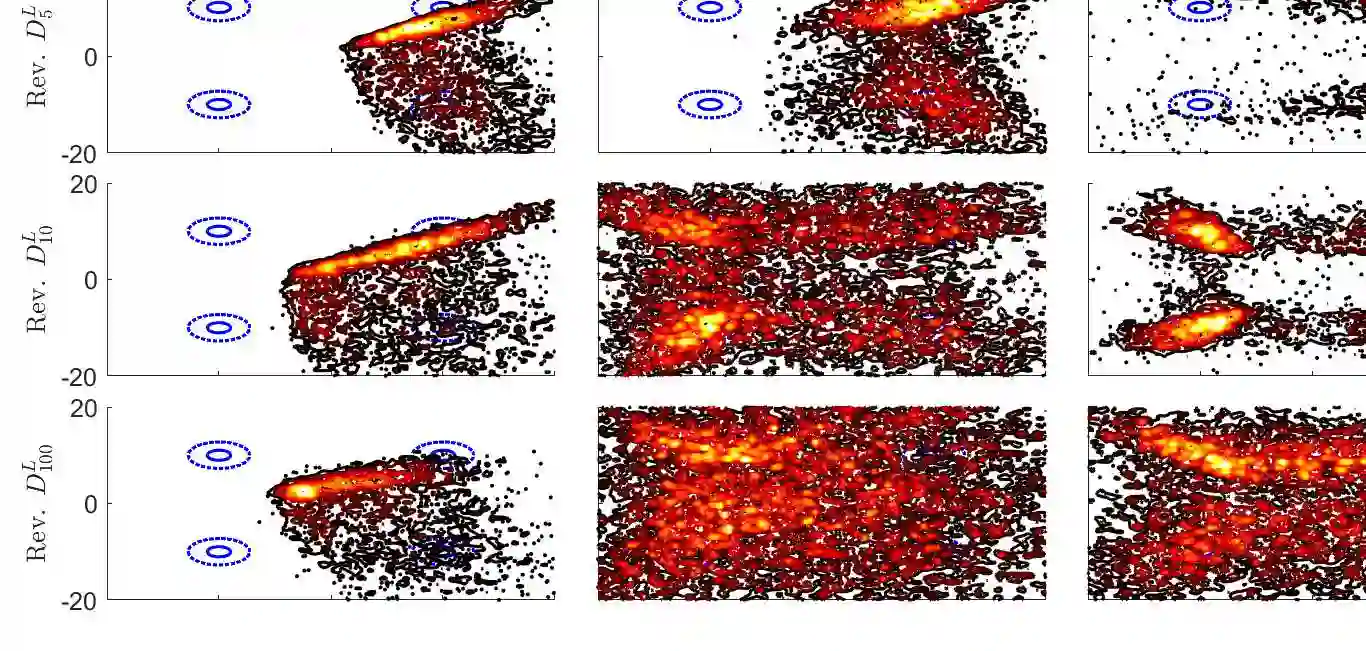
We develop a rigorous and general framework for constructing information-theoretic divergences that subsume both $f$-divergences and integral probability metrics (IPMs), such as the $1$-Wasserstein distance. We prove under which assumptions these divergences, hereafter referred to as $(f,\Gamma)$-divergences, provide a notion of `distance' between probability measures and show that they can be expressed as a two-stage mass-redistribution/mass-transport process. The $(f,\Gamma)$-divergences inherit features from IPMs, such as the ability to compare distributions which are not absolutely continuous, as well as from $f$-divergences, namely the strict concavity of their variational representations and the ability to control heavy-tailed distributions for particular choices of $f$. When combined, these features establish a divergence with improved properties for estimation, statistical learning, and uncertainty quantification applications. Using statistical learning as an example, we demonstrate their advantage in training generative adversarial networks (GANs) for heavy-tailed, not-absolutely continuous sample distributions. We also show improved performance and stability over gradient-penalized Wasserstein GAN in image generation.
翻译:我们为构建信息理论差异制定了严格的总体框架,其中既包括美元差异,又包括美元-瓦瑟斯坦距离等综合概率指标(IPMs),我们证明这些差异所依据的假设是(f,\伽玛)美元差异,以下称为(f,\Gamma)美元差异,提供了概率计量方法之间的“距离”概念,并表明这些差异可以表现为两个阶段的大规模再分配/大众运输过程。$(f,\Gamma)美元差异继承了IPM的特征,例如能够比较并非绝对连续的分布,以及美元差异(f)差异,即其变异表现的严格简洁性,以及控制重压缩分布的能力,具体选择为美元。这些特征加在一起,在估算、统计学习和不确定性量化应用的特性改进后,这些特征就形成了差异。我们以统计学学为例,展示了它们在培训对抗性对准网络(GANs)的优势,这些特征并非绝对持续的连续持续持续持续持续持续持续持续持续持续传播的GASLA图像方面的优势。