FAST-PCA: A Fast and Exact Algorithm for Distributed Principal Component Analysis

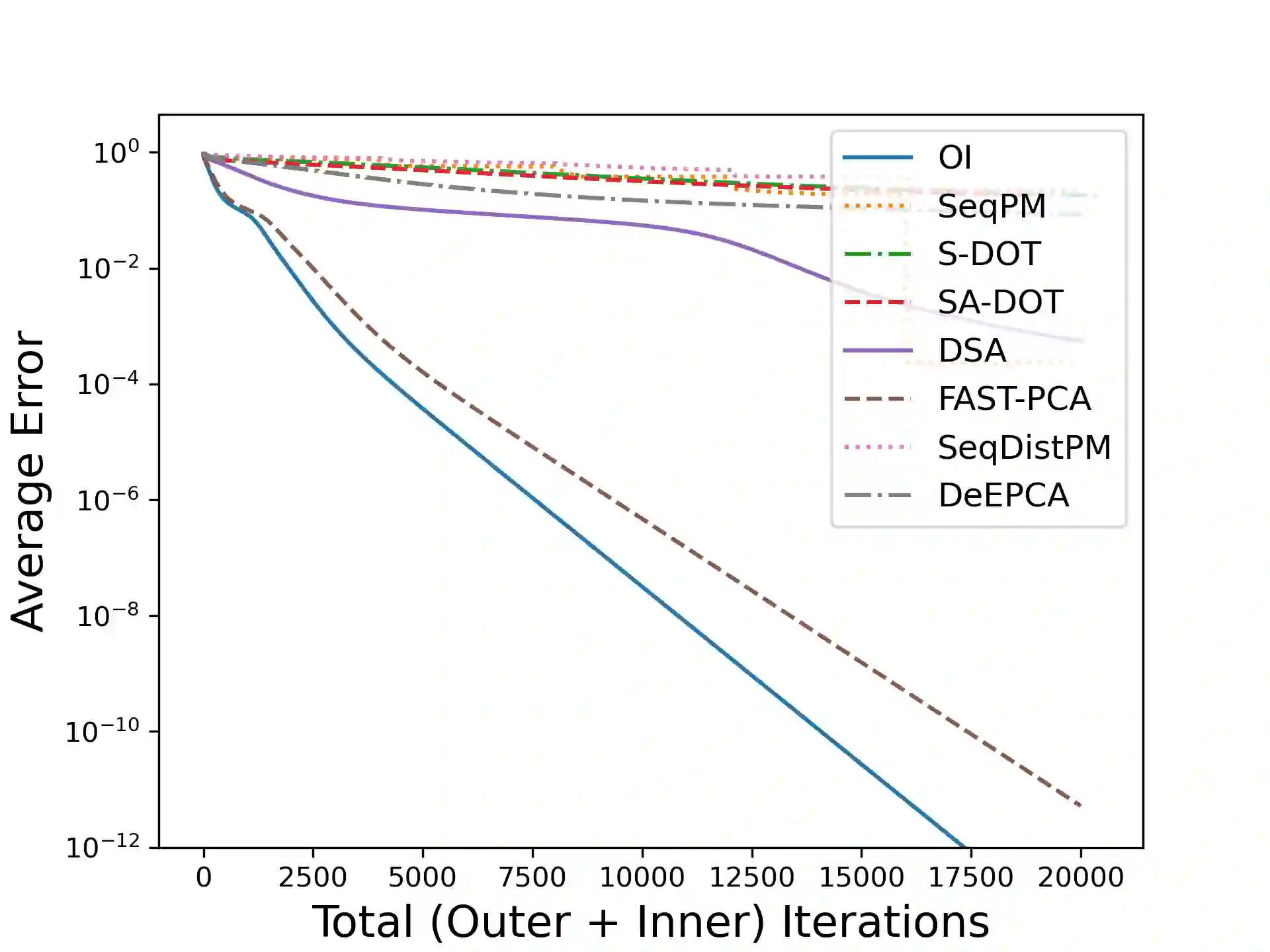
Principal Component Analysis (PCA) is a fundamental data preprocessing tool in the world of machine learning. While PCA is often reduced to dimension reduction, the purpose of PCA is actually two-fold: dimension reduction and feature learning. Furthermore, the enormity of the dimensions and sample size in the modern day datasets have rendered the centralized PCA solutions unusable. In that vein, this paper reconsiders the problem of PCA when data samples are distributed across nodes in an arbitrarily connected network. While a few solutions for distributed PCA exist those either overlook the feature learning part of the purpose, have communication overhead making them inefficient and/or lack exact convergence guarantees. To combat these aforementioned issues, this paper proposes a distributed PCA algorithm called FAST-PCA (Fast and exAct diSTributed PCA). The proposed algorithm is efficient in terms of communication and can be proved to converge linearly and exactly to the principal components that lead to dimension reduction as well as uncorrelated features. Our claims are further supported by experimental results.