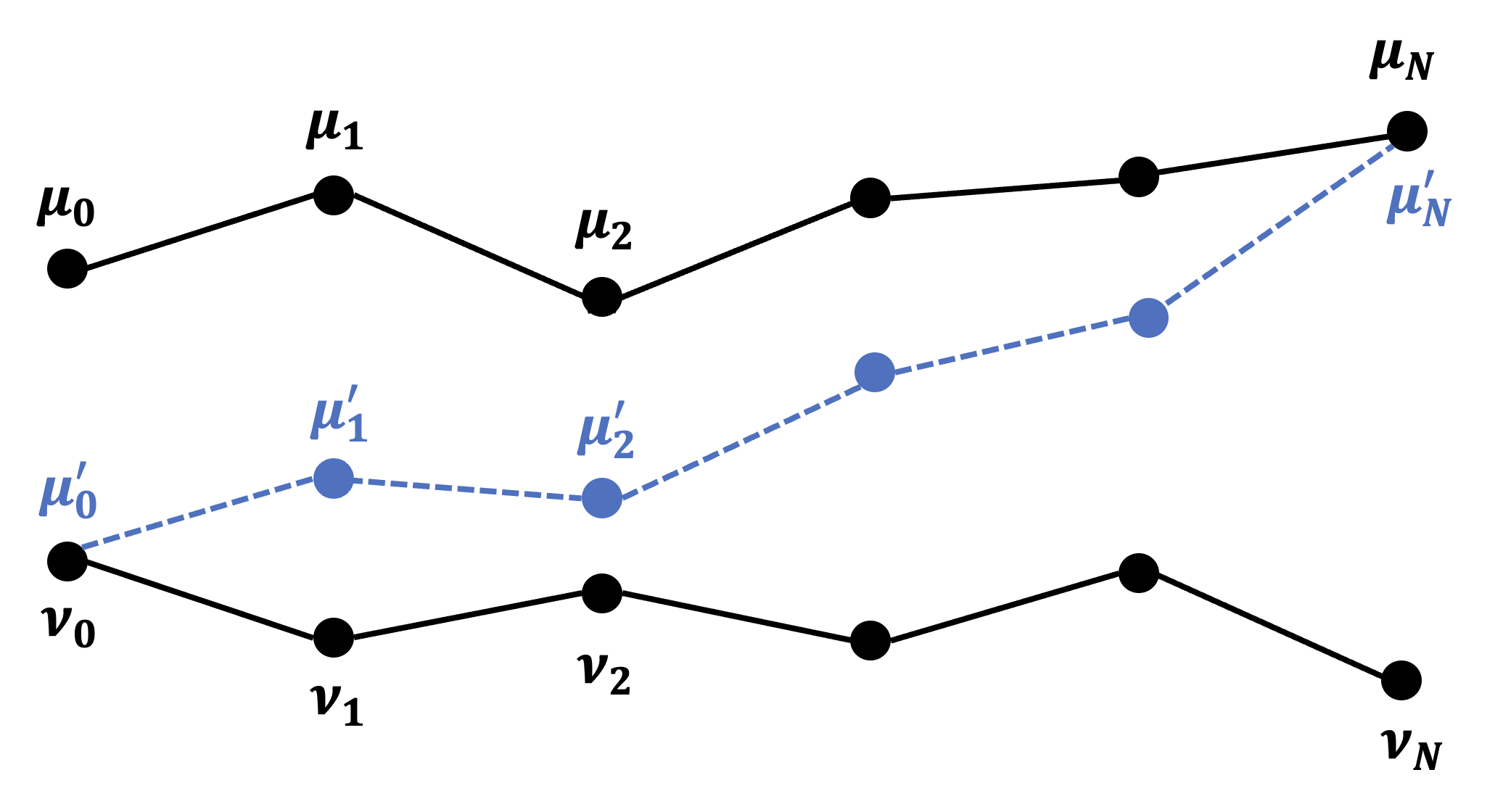
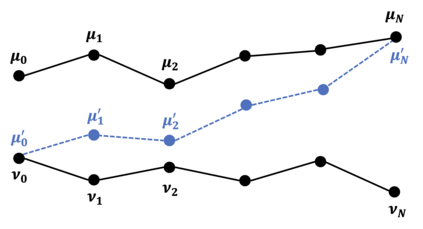
We formulate a new information-theoretic principle--the shifted composition rule--which bounds the divergence (e.g., Kullback-Leibler or R\'enyi) between the laws of two stochastic processes via the introduction of auxiliary shifts. In this paper, we apply this principle to prove reverse transport inequalities for diffusions which, by duality, imply F.-Y. Wang's celebrated dimension-free Harnack inequalities. Our approach bridges continuous-time coupling methods from geometric analysis with the discrete-time shifted divergence technique from differential privacy and sampling. It also naturally gives rise to (1) an alternative continuous-time coupling method based on optimal transport, which bypasses Girsanov transformations, (2) functional inequalities for discrete-time processes, and (3) a family of "reverse" Harnack inequalities.
翻译:暂无翻译