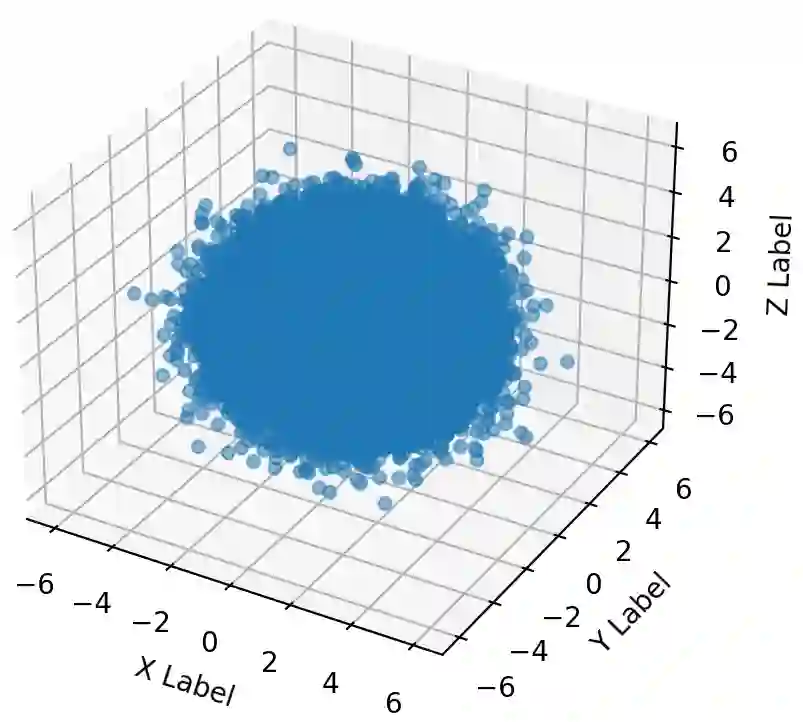
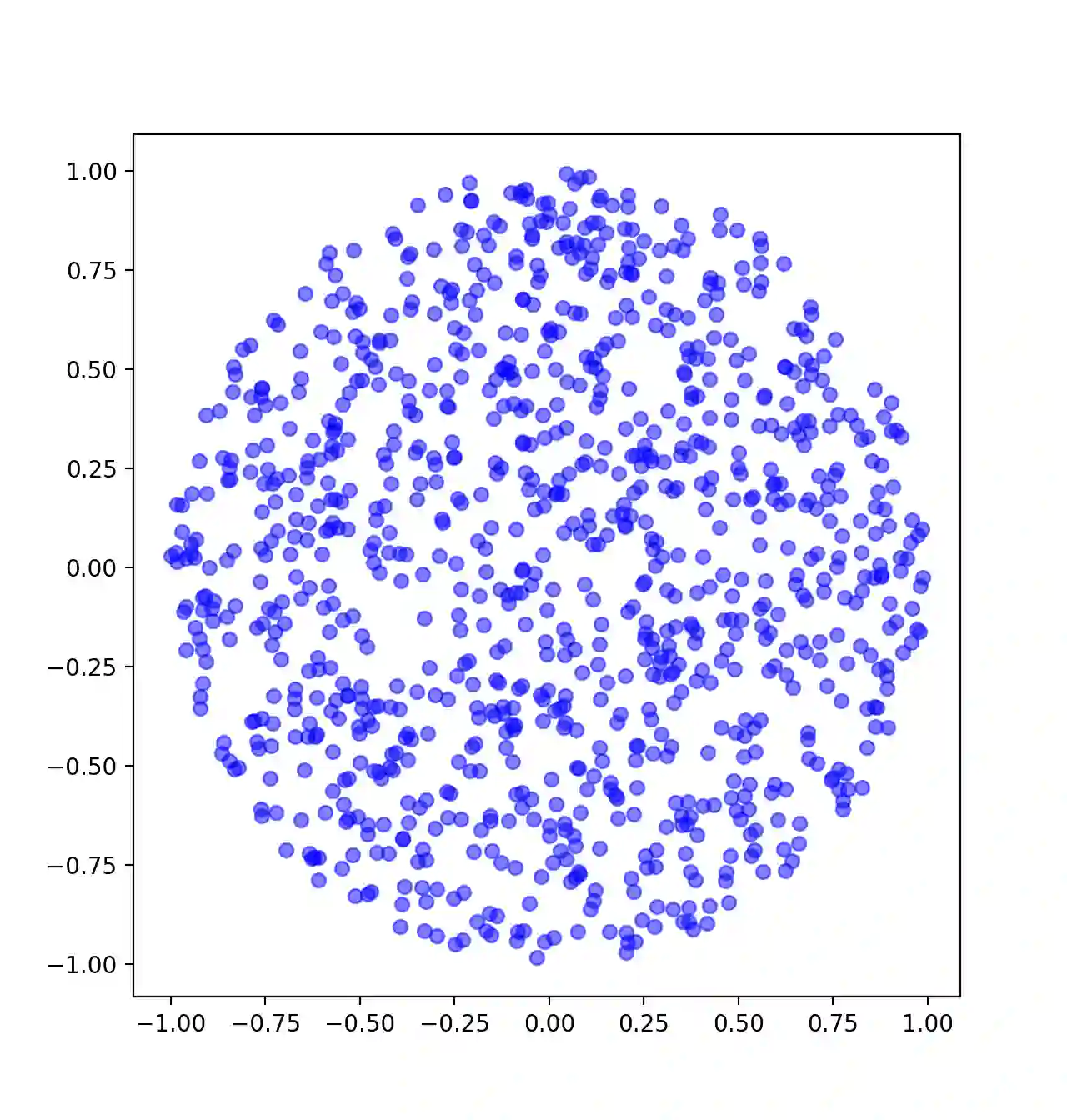
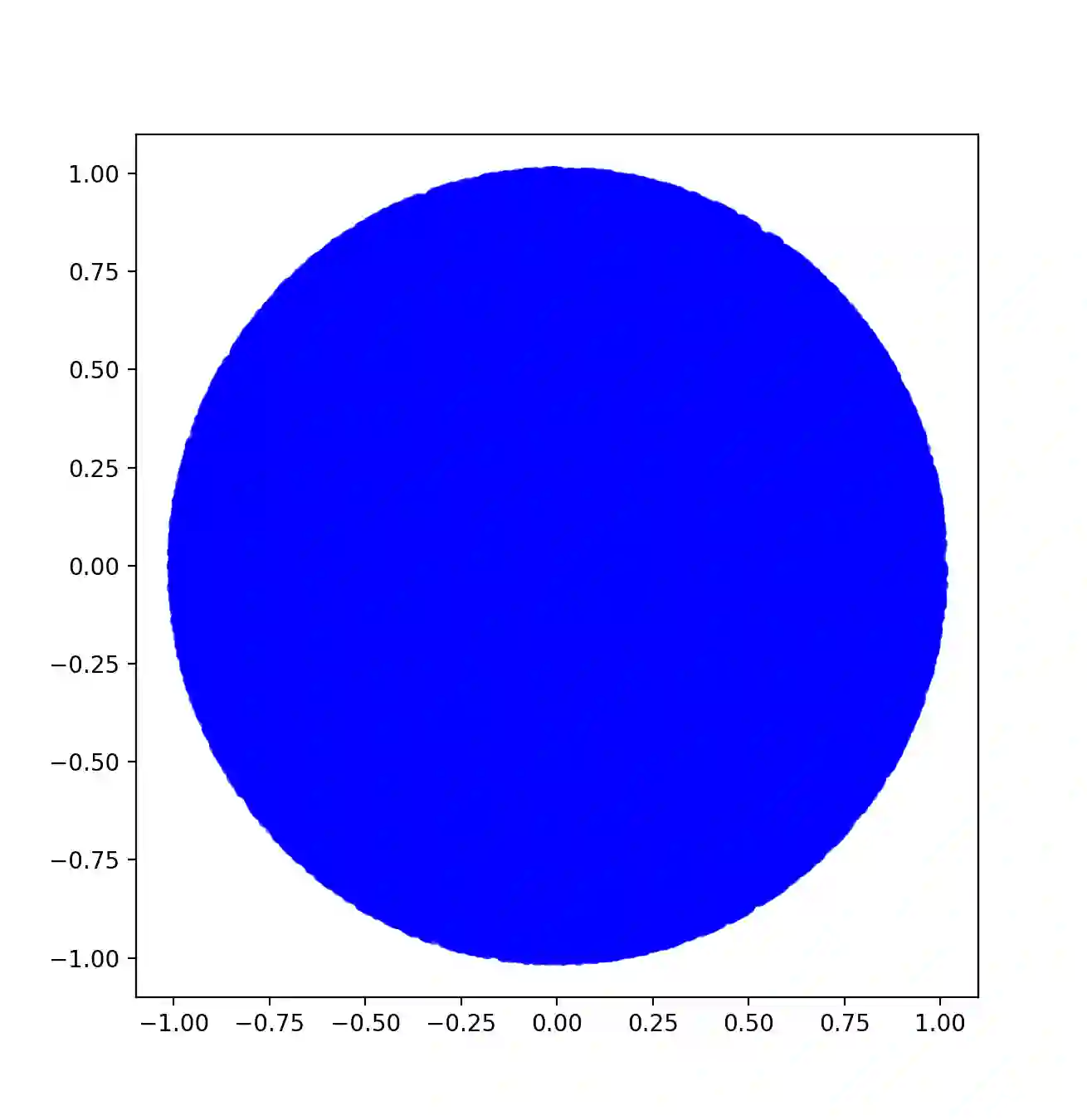
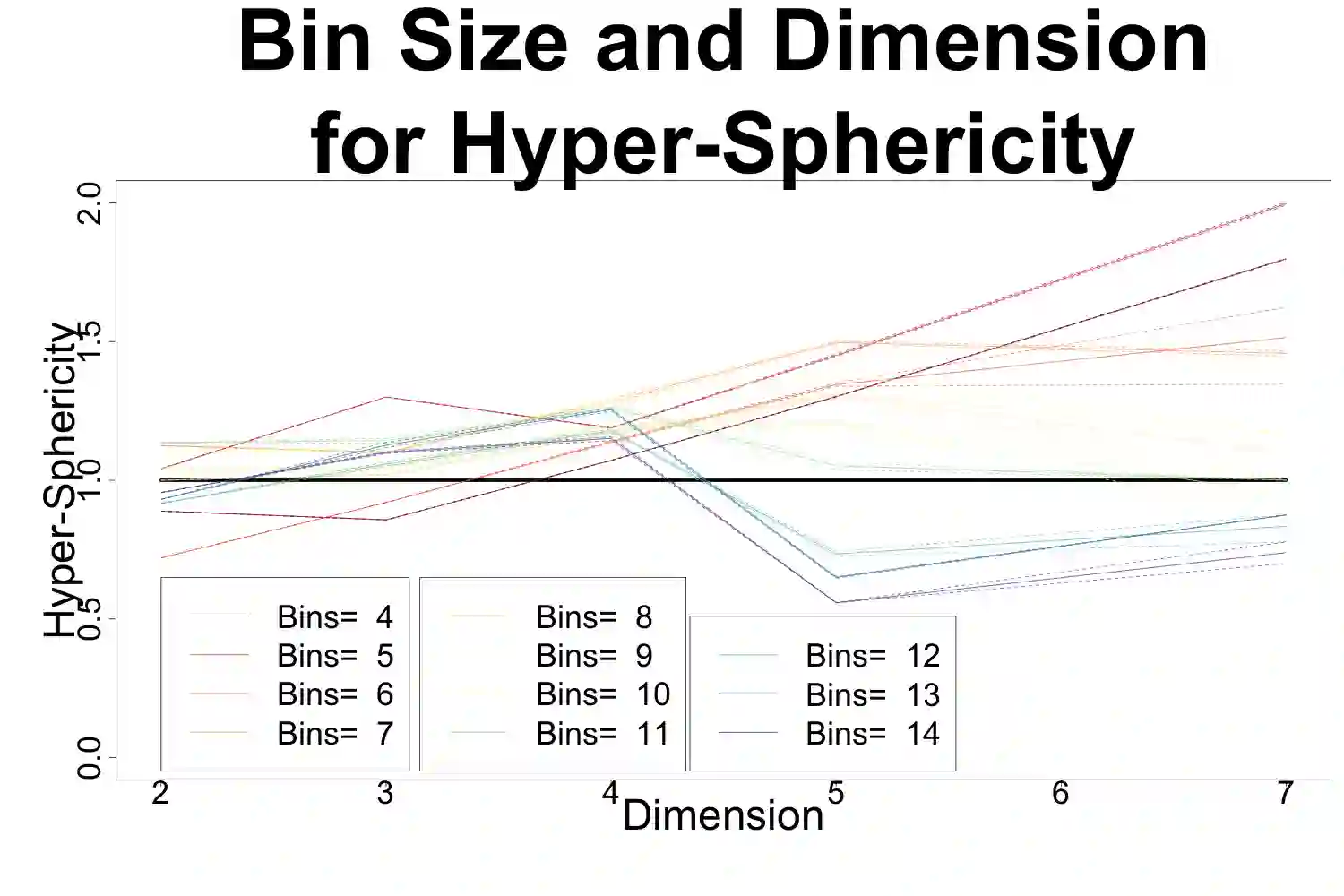
Shape metrics for objects in high dimensions remain sparse. Those that do exist, such as hyper-volume, remain limited to objects that are better understood such as Platonic solids and $n$-Cubes. Further, understanding objects of ill-defined shapes in higher dimensions is ambiguous at best. Past work does not provide a single number to give a qualitative understanding of an object. For example, the eigenvalues from principal component analysis results in $n$ metrics to describe the shape of an object. Therefore, we need a single number which can discriminate objects with different shape from one another. Previous work has developed shape metrics for specific dimensions such as two or three dimensions. However, there is an opportunity to develop metrics for any desired dimension. To that end, we present two new shape metrics for objects in a given number of dimensions: hyper-Sphericity and hyper-Shape Proportion (SP). We explore the proprieties of these metrics on a number of different shapes including $n$-balls. We then connect these metrics to applications of analyzing the shape of multidimensional data such as the popular Iris dataset.
翻译:高维天体的形状测量仪仍然很少。 存在的对象, 如超容量, 仍然局限于更能理解的物体, 如平流固体和美元立方体。 此外, 了解更高维度中定义不清的形状的物体最多是模糊的。 过去的工作没有提供一个单一的数字来提供对一个物体的定性理解。 例如, 主元组成部分分析产生的电子元值以美元计来描述一个对象的形状。 因此, 我们需要一个单一的数字来区分不同形状的物体。 先前的工作已经为两个或三个维度等特定维度制定了形状测量仪。 但是, 有机会为任何理想维度制定测量仪。 为此, 我们为一个特定维度中的天体提供了两个新的形状测量仪: 超光谱和超光谱比例( SP) 。 我们探索这些测量仪在包括 $- ball 在内的不同形状的形状上的特性。 我们然后将这些测量仪与分析诸如广观数据等多维数据形状的应用联系起来。