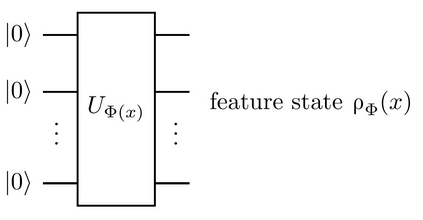
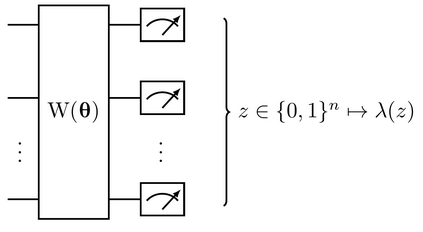
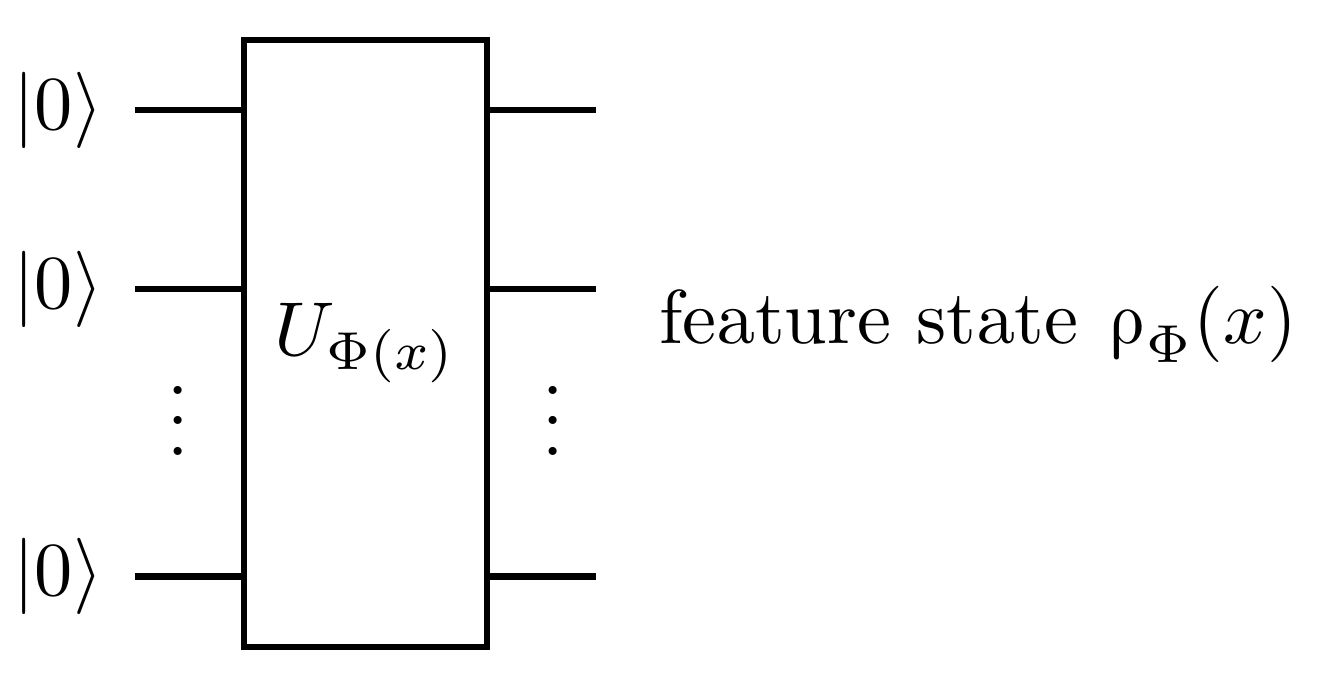
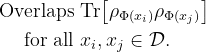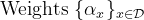Quantum machine learning (QML) stands out as one of the typically highlighted candidates for quantum computing's near-term "killer application". In this context, QML models based on parameterized quantum circuits comprise a family of machine learning models that are well suited for implementations on near-term devices and that can potentially harness computational powers beyond what is efficiently achievable on a classical computer. However, how to best use these models -- e.g., how to control their expressivity to best balance between training accuracy and generalization performance -- is far from understood. In this paper we investigate capacity measures of two closely related QML models called explicit and implicit quantum linear classifiers (also called the quantum variational method and quantum kernel estimator) with the objective of identifying new ways to implement structural risk minimization -- i.e., how to balance between training accuracy and generalization performance. In particular, we identify that the rank and Frobenius norm of the observables used in the QML model closely control the model's capacity. Additionally, we theoretically investigate the effect that these model parameters have on the training accuracy of the QML model. Specifically, we show that there exists datasets that require a high-rank observable for correct classification, and that there exists datasets that can only be classified with a given margin using an observable of at least a certain Frobenius norm. Our results provide new options for performing structural risk minimization for QML models.
翻译:量子机器学习(QML)是量子计算近期“杀手应用”的典型突出候选人之一。在这方面,基于参数化量子电路的QML模型包括一套机器学习模型,这些模型非常适合在近期设备上实施,并有可能利用超越古典计算机有效可实现的计算能力。然而,如何最好地使用这些模型 -- -- 例如,如何控制其表达性,使其在培训准确性和一般化业绩之间取得最佳平衡 -- -- 远未被理解。在本文中,我们调查了两个密切相关的QML模型的能力衡量标准,这两个模型叫明和隐含的量子线性分类器(也称为量子变异法和量内核估测器),目的是确定实施结构风险最小化的新方法,即如何平衡培训准确性和一般化业绩。我们特别确定,QML模型中使用的可观测标准等级和Frobenius规范密切控制模型的能力。此外,我们从理论上调查这些模型对数值最低的量量子线性分类的精确度模型(也称为量子变法度方法和量内值内限值估测测算数据),具体地显示,我们使用某种最低值数据。