D-SVM over Networked Systems with Non-Ideal Linking Conditions

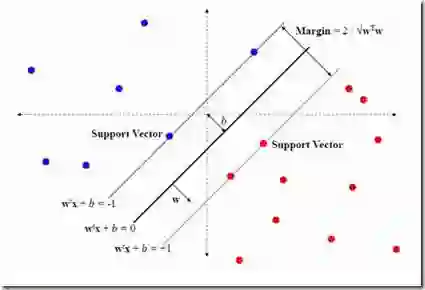
This paper considers distributed optimization algorithms, with application in binary classification via distributed support-vector-machines (D-SVM) over multi-agent networks subject to some link nonlinearities. The agents solve a consensus-constraint distributed optimization cooperatively via continuous-time dynamics, while the links are subject to strongly sign-preserving odd nonlinear conditions. Logarithmic quantization and clipping (saturation) are two examples of such nonlinearities. In contrast to existing literature that mostly considers ideal links and perfect information exchange over linear channels, we show how general sector-bounded models affect the convergence to the optimizer (i.e., the SVM classifier) over dynamic balanced directed networks. In general, any odd sector-bounded nonlinear mapping can be applied to our dynamics. The main challenge is to show that the proposed system dynamics always have one zero eigenvalue (associated with the consensus) and the other eigenvalues all have negative real parts. This is done by recalling arguments from matrix perturbation theory. Then, the solution is shown to converge to the agreement state under certain conditions. For example, the gradient tracking (GT) step size is tighter than the linear case by factors related to the upper/lower sector bounds. To the best of our knowledge, no existing work in distributed optimization and learning literature considers non-ideal link conditions.