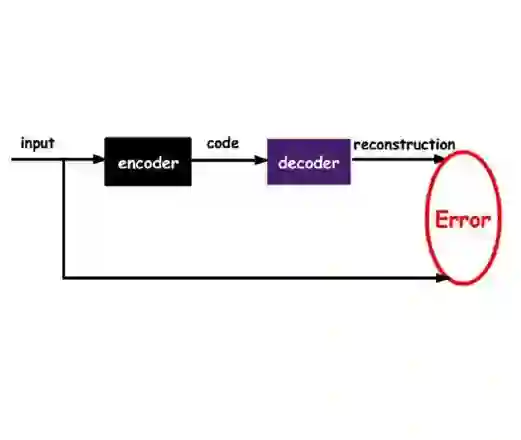
Graph autoencoders (GAEs), as a kind of generative self-supervised learning approach, have shown great potential in recent years. GAEs typically rely on distance-based criteria, such as mean-square-error (MSE), to reconstruct the input graph. However, relying solely on a single reconstruction criterion may lead to a loss of distinctiveness in the reconstructed graph, causing nodes to collapse into similar representations and resulting in sub-optimal performance. To address this issue, we have developed a simple yet effective strategy to preserve the necessary distinctness in the reconstructed graph. Inspired by the knowledge distillation technique, we found that the dual encoder-decoder architecture of GAEs can be viewed as a teacher-student relationship. Therefore, we propose transferring the knowledge of distinctness from the raw graph to the reconstructed graph, achieved through a simple KL constraint. Specifically, we compute pairwise node similarity scores in the raw graph and reconstructed graph. During the training process, the KL constraint is optimized alongside the reconstruction criterion. We conducted extensive experiments across three types of graph tasks, demonstrating the effectiveness and generality of our strategy. This indicates that the proposed approach can be employed as a plug-and-play method to avoid vague reconstructions and enhance overall performance.
翻译:暂无翻译