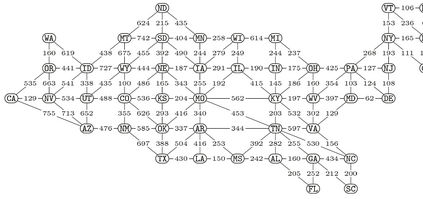
对所有低费用解决方案进行快速计算,对ZDDDs的ZDDs进行双向回溯跟踪 (Interval-Memoized Backtracking on ZDDs for Fast Enumeration of All Lower Cost Solutions)

In many real-life situations, we are often faced with combinatorial problems under linear cost functions. In this paper, we propose a fast method for exactly enumerating a very large number of all lower cost solutions for various combinatorial problems. Our method is based on backtracking for a given decision diagram which represents the feasible solutions of a problem. The main idea is to memoize the intervals of cost bounds to avoid duplicate search in the backtracking process. Although existing state-of-the-art methods with dynamic programming requires a pseudo-polynomial time with the total cost values, it may take an exponential time when the cost values become large. In contrast, the computation time of the proposed method does not directly depend on the total cost values, but is bounded by the input and output size of the decision diagrams. Therefore, it can be much faster than the existing methods if the cost values are large but the output of the decision diagrams are well-compressed. Our experimental results show that, for some practical instances of the Hamiltonian path problem, we succeeded in exactly enumerating billions of all lower cost solutions in a few seconds, which is hundred or more times faster than existing methods. Our method can be regarded as a novel search algorithm which integrates the two classical techniques, branch-and-bound and dynamic programming. This method would have many applications in various fields, including operations research, data mining, statistical testing, hardware/software system design, etc.

翻译：在许多现实环境中,我们往往面临线性成本功能下的组合问题。在本文件中,我们提出一种快速的方法,精确地列出大量各种组合问题的所有较低成本解决方案。我们的方法基于对某决定图的回溯跟踪,该图代表了问题的可行解决方案。主要的想法是,将成本界限的间隔回溯到一起,以避免回溯跟踪过程中的重复搜索。尽管现有最先进的动态程序设计方法需要假的假球时间,总成本值,但当成本值大时,它可能需要一个指数化的时间。相比之下,拟议方法的计算时间并不直接取决于总成本值,而是受决定图的输入和输出大小的约束。因此,如果成本值大,但决定图的输出力受到很好的压缩,它可能比现有方法要快得多。我们的实验结果表明,对于汉密尔顿路问题的一些实际例子,我们成功地在几秒钟内计算出数十亿个低成本解决方案。相比之下,拟议方法的计算时间并不直接取决于总成本值,而是取决于决定图的输入和输出大小。因此,如果成本的计算方法比我们所认为的系统,那么, 的系统—— 模型的系统—— 系统—— 和模型的计算方法—— —— —— 和系统—— 系统—— 系统—— 系统—— 系统—— 系统—— —— 系统—— —— —— —— —— 系统—— 系统—— —— —— —— 系统—— 系统—— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— ——