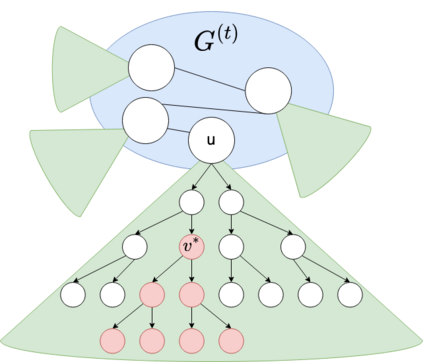
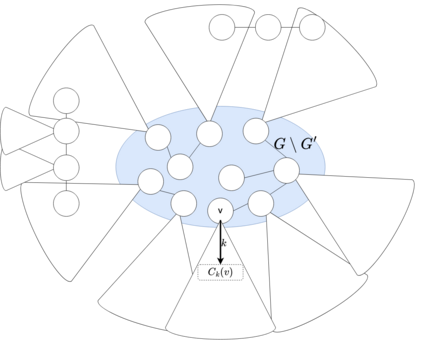
Over the past decade, a long line of research has investigated the distributed complexity landscape of locally checkable labeling (LCL) problems on bounded-degree graphs, culminating in an almost-complete classification on general graphs and a complete classification on trees. The latter states that, on bounded-degree trees, any LCL problem has deterministic worst-case time complexity $O(1)$, $\Theta(\log^* n)$, $\Theta(\log n)$, or $\Theta(n^{1/k})$ for some positive integer $k$, and all of those complexity classes are nonempty. Moreover, randomness helps only for (some) problems with deterministic worst-case complexity $\Theta(\log n)$, and if randomness helps (asymptotically), then it helps exponentially. In this work, we study how many distributed rounds are needed on average per node in order to solve an LCL problem on trees. We obtain a partial classification of the deterministic node-averaged complexity landscape for LCL problems. As our main result, we show that every problem with worst-case round complexity $O(\log n)$ has deterministic node-averaged complexity $O(\log^* n)$. Then we show how using randomization we can speed this up and show that every problem with worst case round complexity $O(\log n)$ has randomized node-averaged complexity $O(1)$. We further establish bounds on the node-averaged complexity of problems with worst-case complexity $\Theta(n^{1/k})$: we show that all these problems have node-averaged complexity $\widetilde{\Omega}(n^{1 / (2^k - 1)})$, and that this lower bound is tight for some problems. The lower bound holds even for the randomized case and the upper bound is a deterministic algorithm.
翻译:暂无翻译