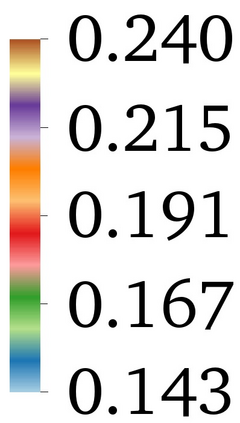
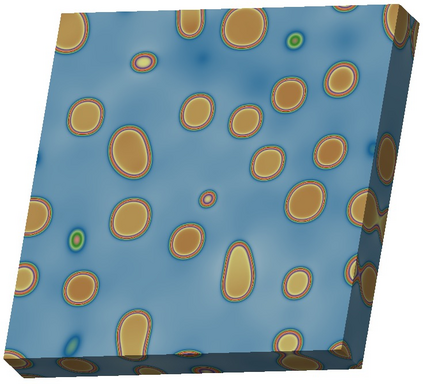
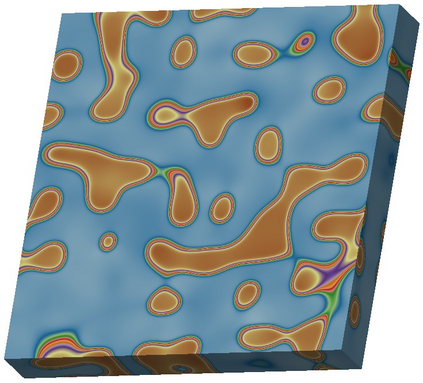
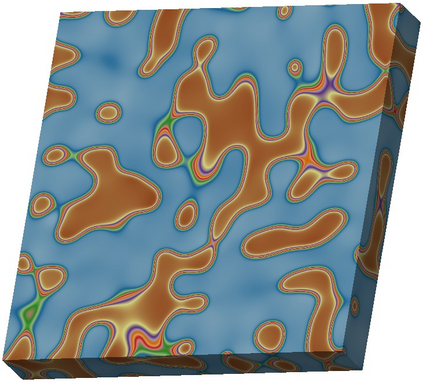
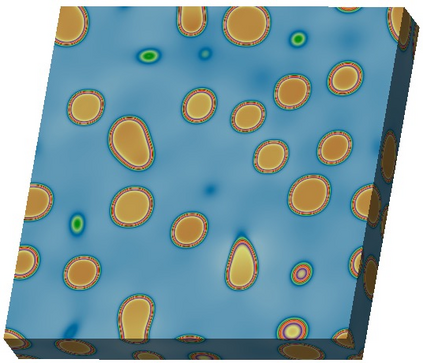
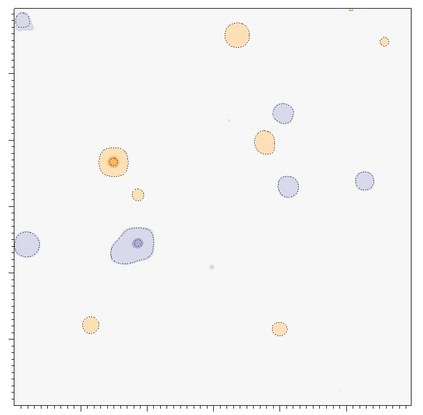
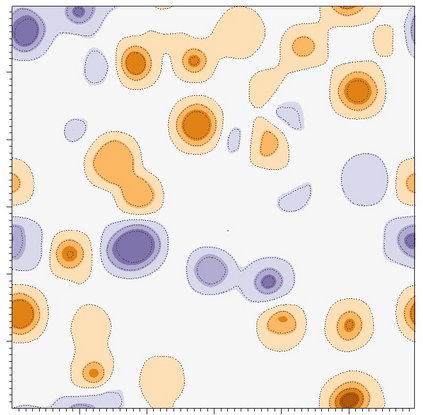
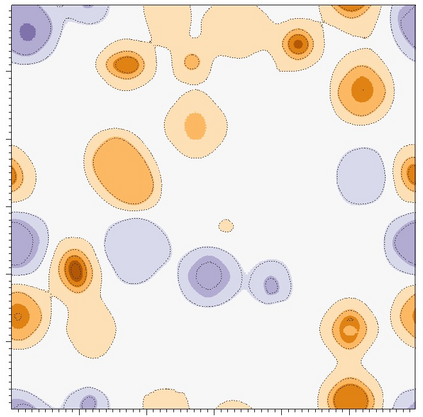
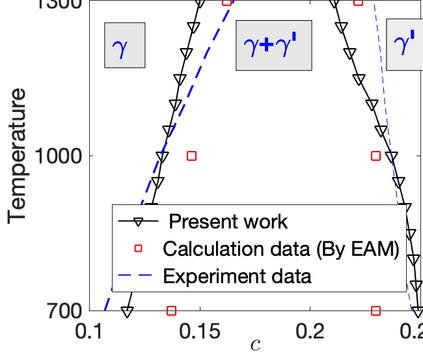
In this paper, we investigate numerical methods for solving Nickel-based phase field system related to free energy, including the elastic energy and logarithmic type functionals. To address the challenge posed by the particular free energy functional, we propose a semi-implicit scheme based on the discrete variational derivative method, which is unconditionally energy stable and maintains the energy dissipation law and the mass conservation law. Due to the good stability of the semi-implicit scheme, the adaptive time step strategy is adopted, which can flexibly control the time step according to the dynamic evolution of the problem. A domain decomposition based, parallel Newton--Krylov--Schwarz method is introduced to solve the nonlinear algebraic system constructed by the discretization at each time step. Numerical experiments show that the proposed algorithm is energy stable with large time steps, and highly scalable to six thousand processor cores.
翻译:在本文中,我们研究了解决与自由能源有关的基于镍的阶段场系统的数字方法,包括弹性能源和对数型功能。为了应对特定自由能源功能带来的挑战,我们提出了一个基于离散变异衍生物法的半隐含办法,该办法无条件的能源稳定,并维持能源消散法和大规模节能法。由于半隐蔽办法的稳定性,采用了适应性时间步骤战略,可以根据问题的动态演变灵活控制时间步骤。采用了基于域分解的平行牛顿-克里洛夫-施瓦兹法,以解决由分解作用在每一步骤中构建的非线性代数系统。数字实验表明,拟议的算法是能源稳定,有大时间步骤,高度可伸缩至6 000个处理核心。