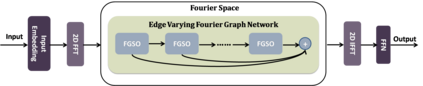
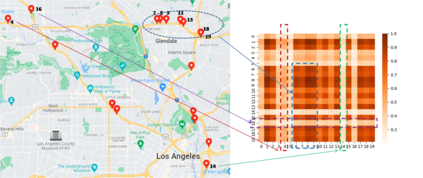
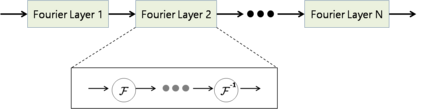
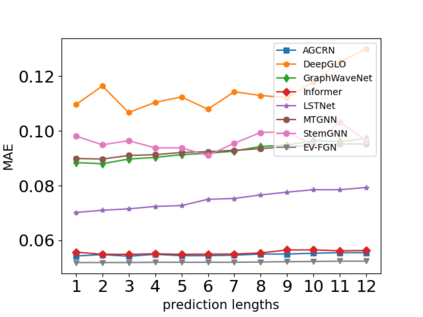
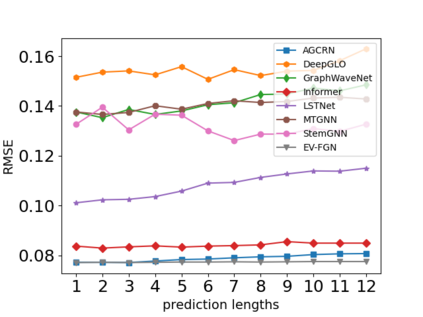
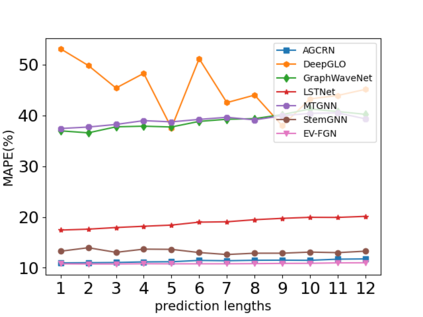
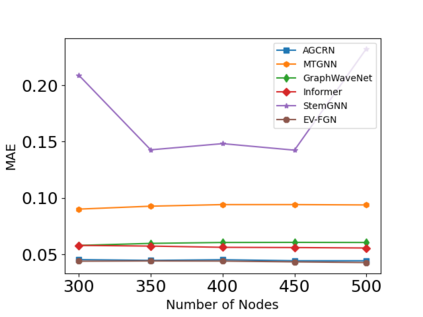
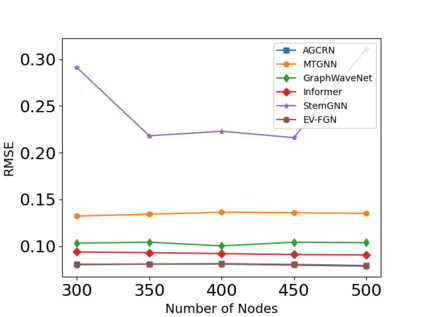
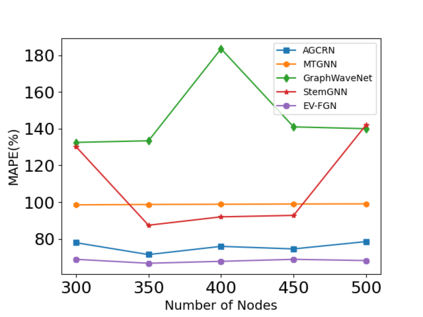
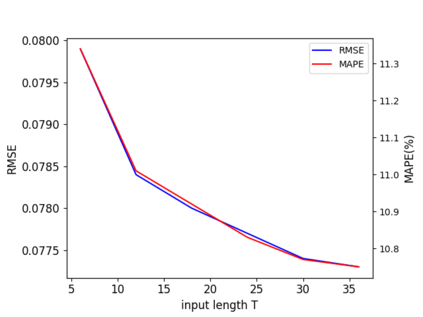
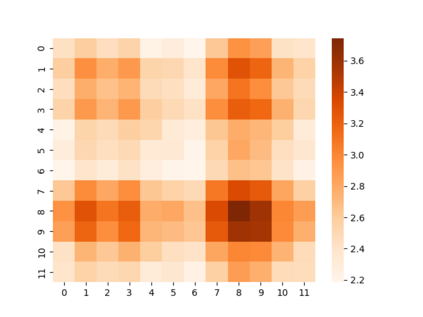
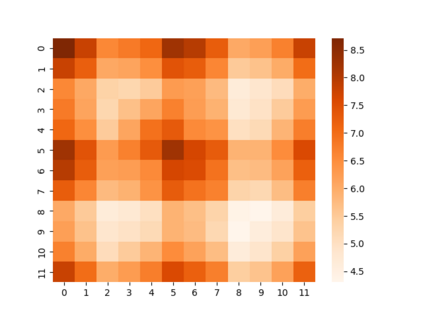
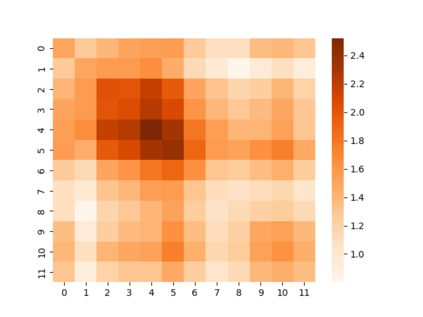
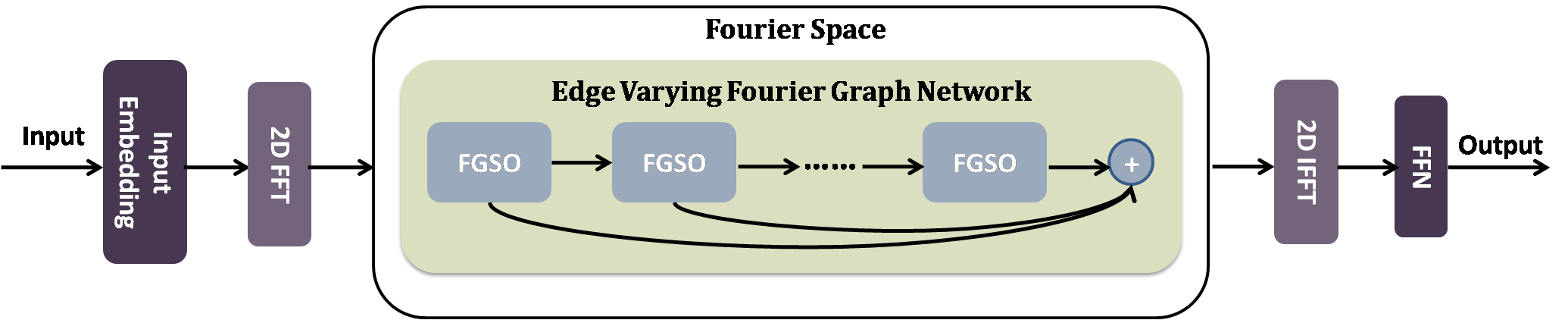
The key problem in multivariate time series (MTS) analysis and forecasting aims to disclose the underlying couplings between variables that drive the co-movements. Considerable recent successful MTS methods are built with graph neural networks (GNNs) due to their essential capacity for relational modeling. However, previous work often used a static graph structure of time-series variables for modeling MTS failing to capture their ever-changing correlations over time. To this end, a fully-connected supra-graph connecting any two variables at any two timestamps is adaptively learned to capture the high-resolution variable dependencies via an efficient graph convolutional network. Specifically, we construct the Edge-Varying Fourier Graph Networks (EV-FGN) equipped with Fourier Graph Shift Operator (FGSO) which efficiently performs graph convolution in the frequency domain. As a result, a high-efficiency scale-free parameter learning scheme is derived for MTS analysis and forecasting according to the convolution theorem. Extensive experiments show that EV-FGN outperforms state-of-the-art methods on seven real-world MTS datasets.
翻译:多变时间序列(MTS)分析和预测的关键问题在于披露驱动共同移动的变量之间的基本组合。最近相当成功的中转方法与图形神经网络(GNNS)一起建立,因为它们具有建立关系模型的基本能力。然而,以往的工作经常使用时间序列变量的静态图形结构来模拟中转系统,但未能捕捉它们随时间变化的关联。为此,在任何两个时标上连接任何两个变量的完全连接的超版图是适应性地学会通过高效的图形相向网络捕捉高分辨率变量依赖性。具体地说,我们建造了配有四面形图转换操作器(FGSO)的EV-VARGNT图网络(EV-FGN),以高效地在频率域进行图变换。结果是,根据相变换的理论,为多边贸易体制分析和预报而制定了一种高效的无比例参数学习计划。广泛的实验显示,EV-FGNT在7个现实世界的MT系统数据组中超越了状态方法。