Implicit Regularization in Over-Parameterized Support Vector Machine

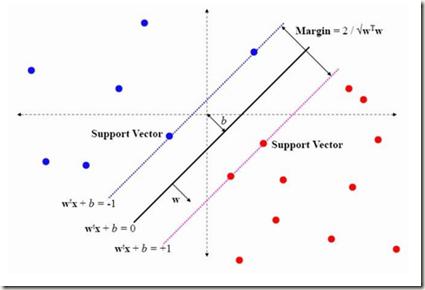
In this paper, we design a regularization-free algorithm for high-dimensional support vector machines (SVMs) by integrating over-parameterization with Nesterov's smoothing method, and provide theoretical guarantees for the induced implicit regularization phenomenon. In particular, we construct an over-parameterized hinge loss function and estimate the true parameters by leveraging regularization-free gradient descent on this loss function. The utilization of Nesterov's method enhances the computational efficiency of our algorithm, especially in terms of determining the stopping criterion and reducing computational complexity. With appropriate choices of initialization, step size, and smoothness parameter, we demonstrate that unregularized gradient descent achieves a near-oracle statistical convergence rate. Additionally, we verify our theoretical findings through a variety of numerical experiments and compare the proposed method with explicit regularization. Our results illustrate the advantages of employing implicit regularization via gradient descent in conjunction with over-parameterization in sparse SVMs.