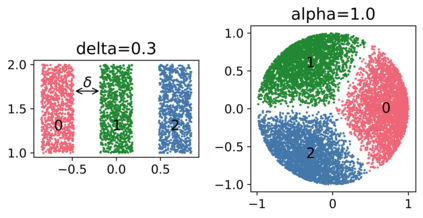
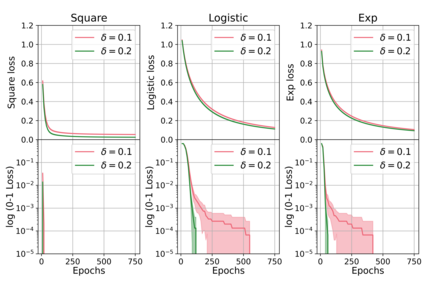
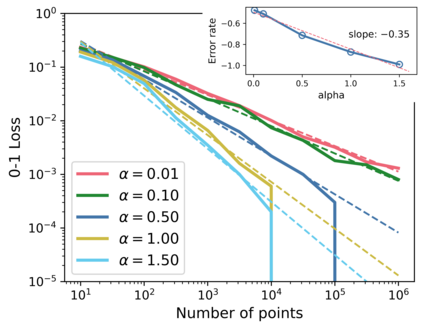
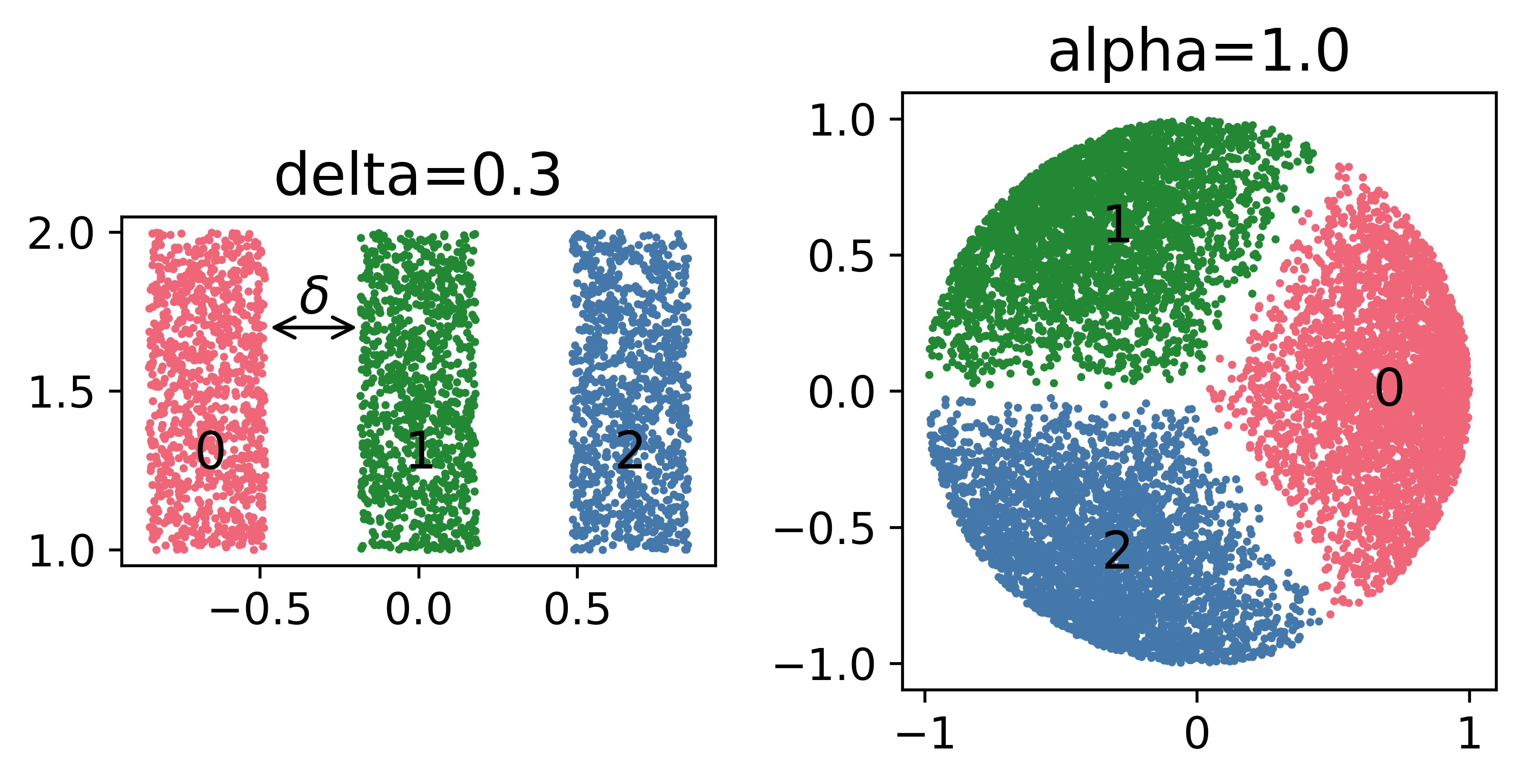
We study the behavior of error bounds for multiclass classification under suitable margin conditions. For a wide variety of methods we prove that the classification error under a hard-margin condition decreases exponentially fast without any bias-variance trade-off. Different convergence rates can be obtained in correspondence of different margin assumptions. With a self-contained and instructive analysis we are able to generalize known results from the binary to the multiclass setting.
翻译:我们研究在适当差值条件下多级分类的误差界限行为。 对于各种各样的方法,我们证明硬差条件下的分类错误在没有任何偏差权衡的情况下会以指数速度快速下降。不同的差值假设可以取得不同的趋同率。通过自成一体和具有启发性的分析,我们可以将已知的结果从二进制推广到多级设置。
相关内容
Arxiv
0+阅读 · 2022年4月20日
Arxiv
1+阅读 · 2022年4月18日
Arxiv
17+阅读 · 2019年9月9日