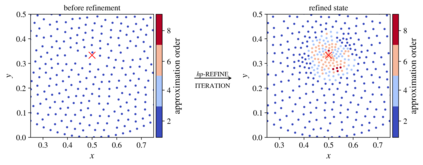
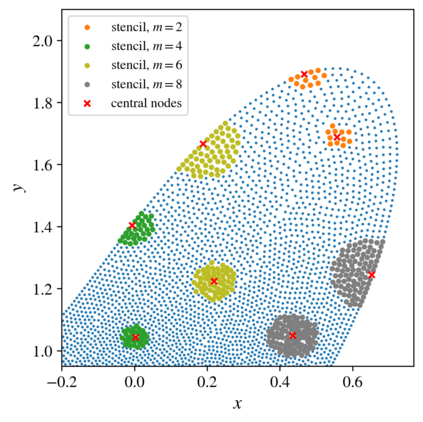
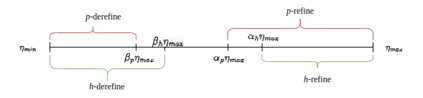
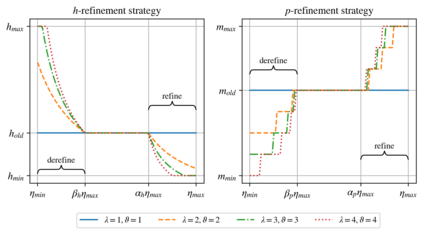
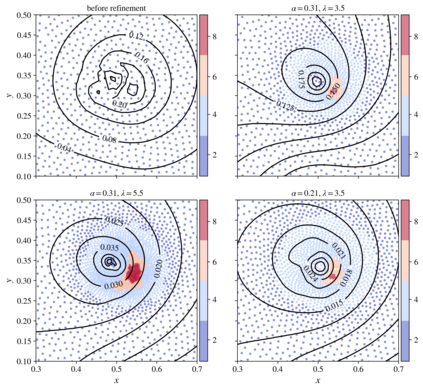
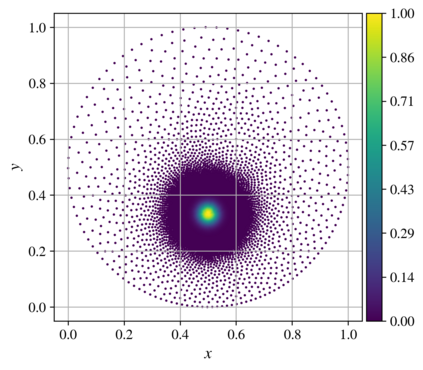
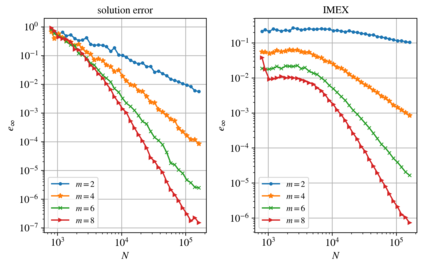
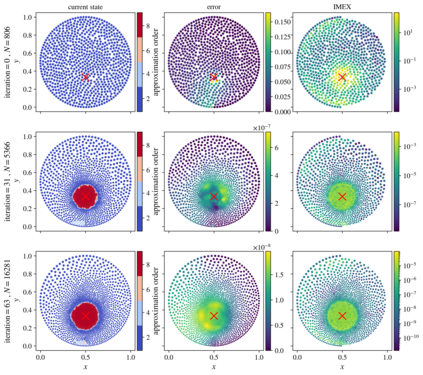
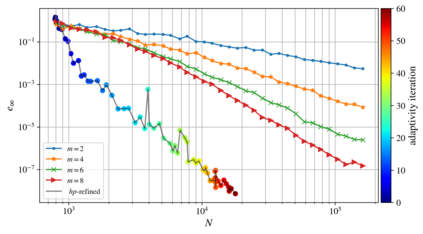
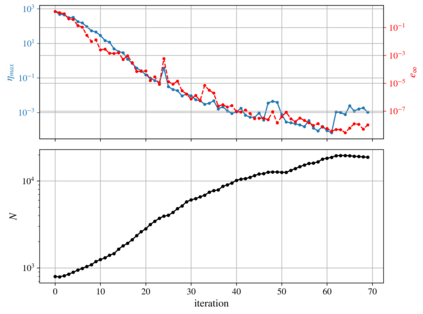
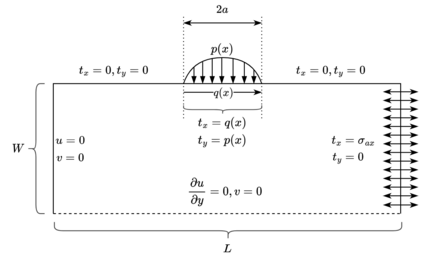
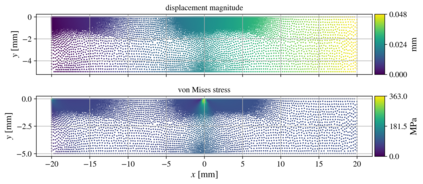
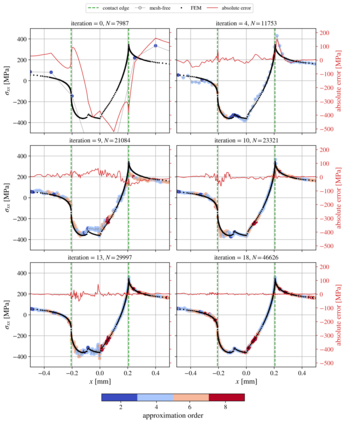
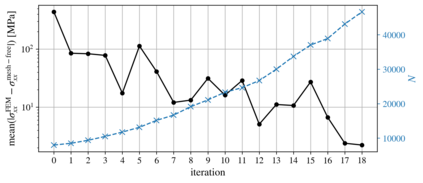
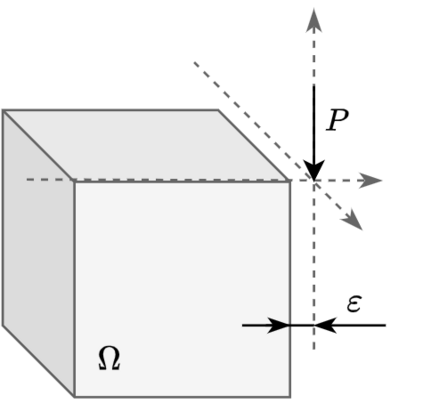
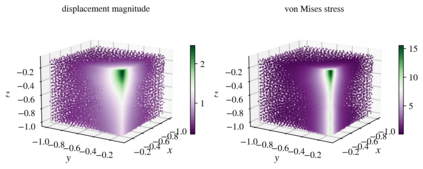
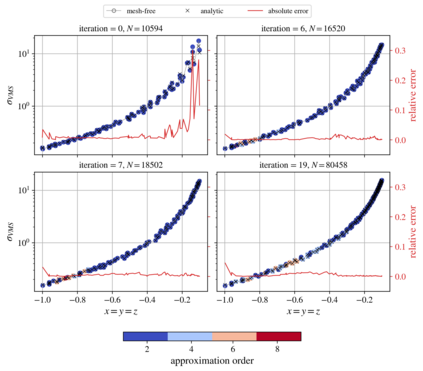
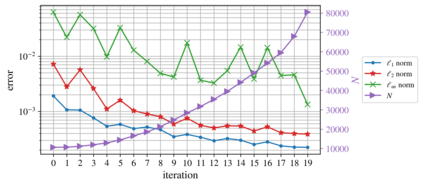
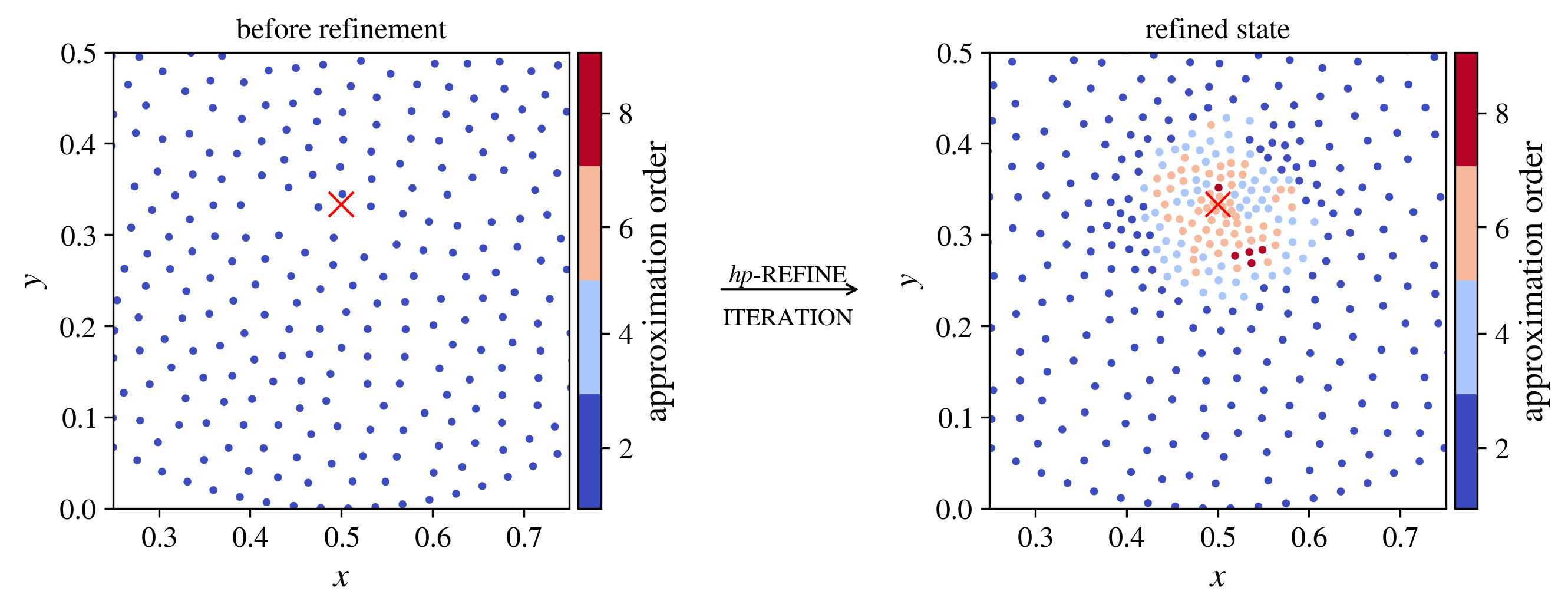
We present an algorithm for $hp$-adaptive collocation-based mesh-free numerical analysis of partial differential equations. Our solution procedure follows a well-established iterative solve-estimate-mark-refine paradigm. The solve phase relies on the Radial Basis Function-generated Finite Differences (RBF-FD) using point clouds generated by advancing front node positioning algorithm that supports variable node density. In the estimate phase, we introduce an Implicit-Explicit (IMEX) error indicator, which assumes that the error relates to the difference between the implicitly obtained solution (from the solve phase) and a local explicit re-evaluation of the PDE at hand using a higher order approximation. Based on the IMEX error indicator, the modified Texas Three Step marking strategy is used to mark the computational nodes for $h$-, $p$- or $hp$-(de-)refinement. Finally, in the refine phase, nodes are repositioned and the order of the method is locally redefined using the variable order of the augmenting monomials according to the instructions from the mark phase. The performance of the introduced $hp$-adaptive method is first investigated on a two-dimensional Peak problem and further applied to two- and three-dimensional contact problems. We show that the proposed IMEX error indicator adequately captures the global behaviour of the error in all cases considered and that the proposed $hp$-adaptive solution procedure significantly outperforms the non-adaptive approach. The proposed $hp$-adaptive method stands for another important step towards a fully autonomous numerical method capable of solving complex problems in realistic geometries without the user intervention.
翻译:在估算阶段,我们提出了一个隐含的(IMEX)误差指标,它假定错误与隐含获得的解决方案(从解析阶段)与使用更高的自动排序近似值对手边的PDE进行当地明确重新评价之间存在的差异有关。根据IMEX误差指标,经修订的德克萨斯三步标记战略用于标记支持可变节点密度的前节点定位算法生成的计算节点。最后,在精细阶段,对节点进行重新定位,该方法的顺序在当地重新定义,根据标志阶段的指示,对手边的PDE进行当地明确的重新评价。根据IMEX误差指标,修改的德克萨斯三步标记战略用于标记美元、美元或美元或美元-(de)再精确度的计算节点。最后,在精细阶段,对节点进行重新定位,对方法的顺序进行重新定义,根据标志阶段的指示,对手边的PDE进行当地明确的重新评价。在IMEX误差指标阶段,对二维基的用户方法进行了进一步测试。